题目内容
19.如图,已知三棱锥S-ABC中,侧棱SA=SB=SC,又有∠ABC=90°,求证:平面ABC⊥平面ASC.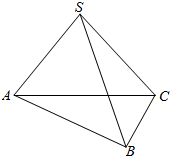
分析 作SH⊥AC交AC于点H,由线面垂直的判定定理,可得SH⊥平面ABC,再由面面垂直的判定定理,即可得证.
解答  证明:作SH⊥AC交AC于点H,
证明:作SH⊥AC交AC于点H,
∵SA=SC,
∴AH=HC.
在Rt△ABC中,H是AC的中点,
∴BH=$\frac{1}{2}$AC=AH,
又SH=SH,SA=SB,
∴△SAH≌△SBH(SSS),
∴SH⊥BH,
又AC∩BH=H,
∴SH⊥平面ABC,
又SH?平面ASC,
∴平面ABC⊥平面ASC.
点评 本题考查面面垂直的判定定理的运用,考查空间线面的位置关系,属于中档题.

练习册系列答案
相关题目
9.已知变量x,y满足约束条件$\left\{{\begin{array}{l}{x+y≥1}\\{3x+y≤3}\\{x≥0}\end{array}}\right.$,则目标函数z=2x+y的最小值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
11.已知不等式x2+px+q<0的解集是-3<x<2,则( )
| A. | p=-1,q=6 | B. | p=1,q=6 | C. | p=-1,q=-6 | D. | p=1,q=-6 |