题目内容
已知曲线C的方程为:ax2+ay2-2a2x-4y=0(a≠0,a为常数).
(1)判断曲线C的形状;
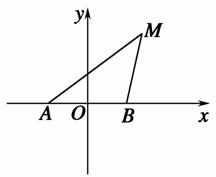
(2)设曲线C分别与x轴,y轴交于点A,B(A,B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;
(3)设直线l:y=-2x+4与曲线C交于不同的两点M,N,且|OM|=|ON|,求曲线C的方程.
解 (1)将曲线C的方程化为x2+y2-2ax-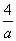 y=0⇒(x-a)2+
y=0⇒(x-a)2+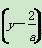 2=a2+
2=a2+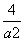 ,可知曲线C是以点
,可知曲线C是以点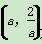 为圆心,以
为圆心,以 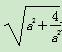 为半径的圆.
为半径的圆.
(2)△AOB的面积S为定值.
证明如下:
在曲线C的方程中令y=0,得ax(x-2a)=0,得点A(2a,0),
在曲线C方程中令x=0,得y(ay-4)=0,得点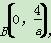
∴S=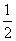 |OA|·|OB|=
|OA|·|OB|=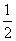 ·|2a|·
·|2a|· =4(定值).
=4(定值).
(3)∵圆C过坐标原点,且|OM|=|ON|,
∴OC⊥MN,∴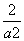 =
=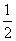 ,∴a=±2.
,∴a=±2.
当a=-2时,圆心坐标为(-2,-1),圆的半径为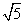 ,
,
圆心到直线l:y=-2x+4的距离
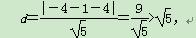 直线l与圆C相离,不合题意舍去,
直线l与圆C相离,不合题意舍去,
∴a=2时符合题意.
这时曲线C的方程为x2+y2-4x-2y=0.

练习册系列答案
相关题目

 的值为( )
的值为( )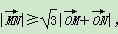 ,其中O是坐标原点,则实数m的取值范围是( )
,其中O是坐标原点,则实数m的取值范围是( )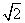 ,-
,-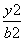 =1(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A,B两点.若|AF1|=3|F1B|,AF2⊥x轴,则椭圆E的方程为________.
=1(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A,B两点.若|AF1|=3|F1B|,AF2⊥x轴,则椭圆E的方程为________.