题目内容
(本小题满分14分)已知函数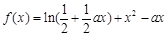 (
(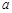 为常数,
为常数,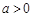 ).
).
(Ⅰ)若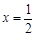 是函数
是函数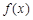 的一个极值点,求
的一个极值点,求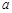 的值;
的值;
(Ⅱ)求证:当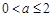 时,
时,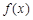 在
在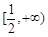 上是增函数;
上是增函数;
(Ⅲ)若对任意的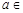 (1,2),总存在
(1,2),总存在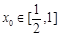 ,使不等式
,使不等式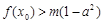 成立,求实数
成立,求实数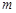 的取范围.
的取范围.
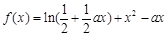 (
(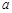 为常数,
为常数,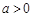 ).
).(Ⅰ)若
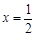 是函数
是函数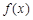 的一个极值点,求
的一个极值点,求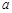 的值;
的值;(Ⅱ)求证:当
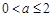 时,
时,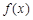 在
在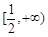 上是增函数;
上是增函数;(Ⅲ)若对任意的
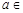 (1,2),总存在
(1,2),总存在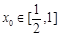 ,使不等式
,使不等式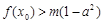 成立,求实数
成立,求实数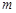 的取范围.
的取范围.(Ⅰ)
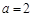 满足条件;(Ⅱ)
满足条件;(Ⅱ)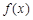 在
在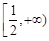 上是增函数;(Ⅲ)实数
上是增函数;(Ⅲ)实数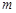 的取值范围为
的取值范围为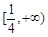 .
.本试题主要是考查了导数在研究函数中的运用。以及不等是的求解,和函数单调性的判定的综合运用。
(1)因为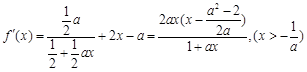
由已知,得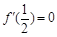 即
即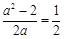 , 得到a的值,
, 得到a的值,
(2)当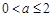 时,
时,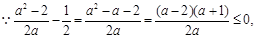
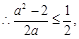
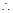 当
当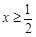 时,
时,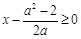 .又
.又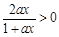 ,
,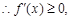 故
故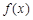 在
在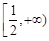 上是增函数
上是增函数
(3)当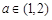 时,由(Ⅱ)知,
时,由(Ⅱ)知,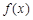 在
在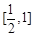 上的最大值为
上的最大值为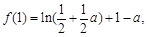
于是问题等价于:对任意的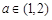 ,不等式
,不等式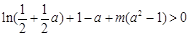 恒成立.
恒成立.
利用构造函数得到结论。
解: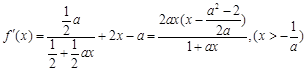 ……………1分
……………1分
(Ⅰ)由已知,得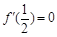 即
即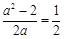 ,
,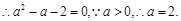 ……3分
……3分
经检验,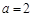 满足条件.……………………………………4分
满足条件.……………………………………4分
(Ⅱ)当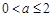 时,
时,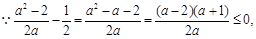
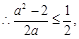 …………5分
…………5分
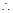 当
当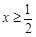 时,
时,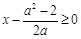 .又
.又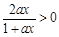 ,
,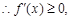 故
故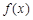 在
在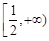 上是增函数
上是增函数
(Ⅲ)当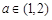 时,由(Ⅱ)知,
时,由(Ⅱ)知,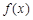 在
在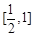 上的最大值为
上的最大值为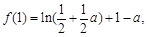
于是问题等价于:对任意的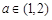 ,不等式
,不等式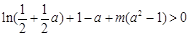 恒成立.
恒成立.
记
则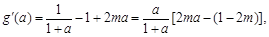 …………………………9分
…………………………9分
当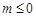 时,有
时,有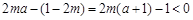 ,且
,且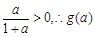 在区间(1,2)上递减,且
在区间(1,2)上递减,且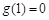 ,则
,则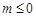 不可能使
不可能使 恒成立,故必有
恒成立,故必有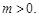 …………11分
…………11分
当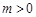 ,且
,且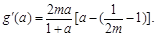
若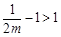 ,可知
,可知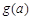 在区间
在区间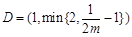 上递减,在此区间
上递减,在此区间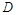 上有
上有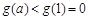 ,与
,与 恒成立矛盾,故
恒成立矛盾,故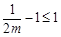 ,这时
,这时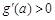 ,即
,即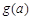 在(1,2)上递增,恒有
在(1,2)上递增,恒有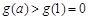 满足题设要求.
满足题设要求.
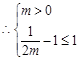 ,即
,即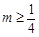 ,所以,实数
,所以,实数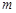 的取值范围为
的取值范围为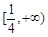 .……………………14分
.……………………14分
(1)因为
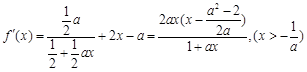
由已知,得
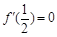 即
即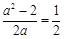 , 得到a的值,
, 得到a的值,(2)当
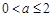 时,
时,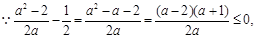
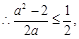
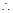 当
当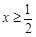 时,
时,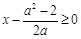 .又
.又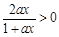 ,
,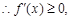 故
故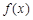 在
在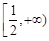 上是增函数
上是增函数(3)当
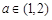 时,由(Ⅱ)知,
时,由(Ⅱ)知,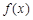 在
在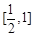 上的最大值为
上的最大值为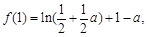
于是问题等价于:对任意的
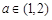 ,不等式
,不等式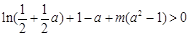 恒成立.
恒成立.利用构造函数得到结论。
解:
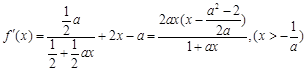 ……………1分
……………1分(Ⅰ)由已知,得
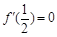 即
即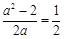 ,
,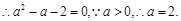 ……3分
……3分经检验,
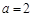 满足条件.……………………………………4分
满足条件.……………………………………4分(Ⅱ)当
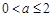 时,
时,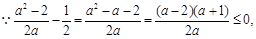
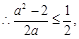 …………5分
…………5分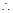 当
当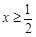 时,
时,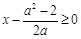 .又
.又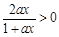 ,
,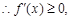 故
故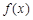 在
在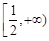 上是增函数
上是增函数(Ⅲ)当
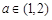 时,由(Ⅱ)知,
时,由(Ⅱ)知,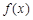 在
在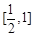 上的最大值为
上的最大值为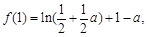
于是问题等价于:对任意的
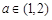 ,不等式
,不等式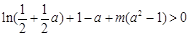 恒成立.
恒成立.记

则
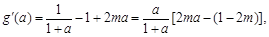 …………………………9分
…………………………9分当
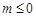 时,有
时,有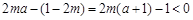 ,且
,且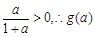 在区间(1,2)上递减,且
在区间(1,2)上递减,且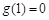 ,则
,则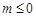 不可能使
不可能使 恒成立,故必有
恒成立,故必有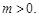 …………11分
…………11分当
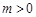 ,且
,且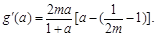
若
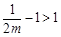 ,可知
,可知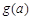 在区间
在区间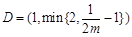 上递减,在此区间
上递减,在此区间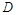 上有
上有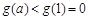 ,与
,与 恒成立矛盾,故
恒成立矛盾,故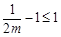 ,这时
,这时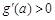 ,即
,即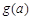 在(1,2)上递增,恒有
在(1,2)上递增,恒有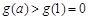 满足题设要求.
满足题设要求.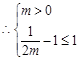 ,即
,即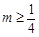 ,所以,实数
,所以,实数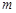 的取值范围为
的取值范围为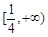 .……………………14分
.……………………14分
练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
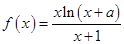
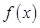 在
在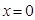 处取到极值,求
处取到极值,求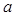 的值.
的值.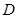 上的函数
上的函数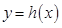 在点
在点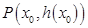 处的切线方程为
处的切线方程为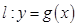 ,若
,若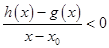 在
在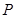 为函数的
为函数的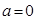 时,试问函数
时,试问函数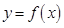 是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.
是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.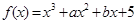 ,过曲线
,过曲线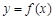 上的点
上的点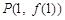 的切线斜率为3.
的切线斜率为3.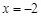 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;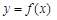 在
在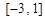 上最大值;
上最大值;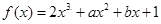 的导数为
的导数为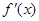 ,若函数
,若函数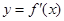 的图像关于直线
的图像关于直线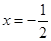 对称,且
对称,且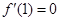 .
.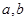 的值(Ⅱ)求函数
的值(Ⅱ)求函数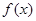 的极值
的极值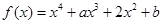 ,
,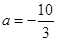 时,讨论函数
时,讨论函数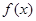 的单调性;
的单调性;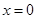 处有极值,试求
处有极值,试求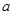 的取值范围。
的取值范围。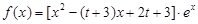 ,
,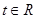
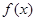 在
在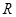 上无极值,求
上无极值,求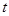 值;
值;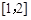 上的最小值
上的最小值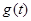 表达式;
表达式;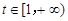 ,任意的
,任意的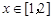 ,均有
,均有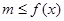 成立,求
成立,求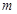 的取值范围.
的取值范围.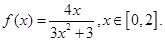
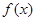 的值域;
的值域;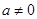 ,函数
,函数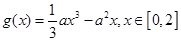 .若对任意
.若对任意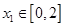 ,总存在
,总存在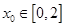 ,使
,使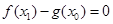 ,求实数
,求实数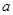 的取值范围.
的取值范围.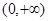 上为增函数的是 ( )
上为增函数的是 ( )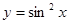
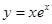
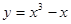
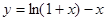
 )
)