题目内容
(12分)函数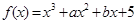 ,过曲线
,过曲线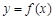 上的点
上的点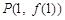 的切线斜率为3.
的切线斜率为3.
(1)若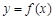 在
在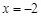 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;
(2)在(1)的条件下,求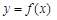 在
在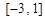 上最大值;
上最大值;
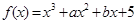 ,过曲线
,过曲线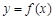 上的点
上的点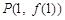 的切线斜率为3.
的切线斜率为3.(1)若
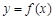 在
在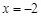 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;(2)在(1)的条件下,求
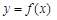 在
在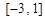 上最大值;
上最大值;(1)a=2,b=-4;(2) 上最大值为13
上最大值为13
 上最大值为13
上最大值为13 本试题主要是考查了导数在研究函数中的运用,研究函数的极值问题,和函数在给定闭区间的最值的综合运用。
(1)利用函数在某点处取得极值,可知在该点处导数为零,同时可以知道函数值,那么得到函数的解析式。
(2)在第一问的基础上,明确的函数解析式,然后求解导数,利用导数大于零和小于零得到函数的单调性,然后确定处极值,比较端点值和极值的大小关系,确定出最值即可。
解:(1)a=2,b=-4
(2)


 上最大值为13
上最大值为13
(1)利用函数在某点处取得极值,可知在该点处导数为零,同时可以知道函数值,那么得到函数的解析式。
(2)在第一问的基础上,明确的函数解析式,然后求解导数,利用导数大于零和小于零得到函数的单调性,然后确定处极值,比较端点值和极值的大小关系,确定出最值即可。
解:(1)a=2,b=-4
(2)

| x |  | -2 |  |  |  |
 | + | 0 | - | 0 | + |
 |  | 极大 |  | 极小 |  |


 上最大值为13
上最大值为13 
练习册系列答案
相关题目
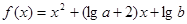 满足
满足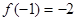 且对于任意
且对于任意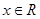 , 恒有
, 恒有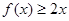 成立
成立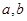 的值; (2)解不等式
的值; (2)解不等式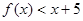
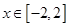 时,函数
时,函数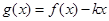 是单调函数,求实数
是单调函数,求实数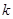 的取值范围。
的取值范围。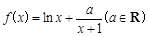 .
.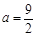 时,如果函数
时,如果函数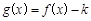 仅有一个零点,求实数
仅有一个零点,求实数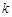 的取值范围;
的取值范围;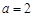 时,试比较
时,试比较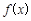 与1的大小;
与1的大小;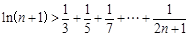
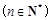 .
.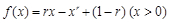 ,其中
,其中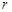 为有理数,且
为有理数,且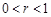 . 求
. 求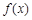 的最小值;
的最小值;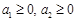 ,
,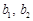 为正有理数. 若
为正有理数. 若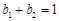 ,则
,则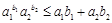 ;
;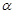 为正有理数时,有求导公式
为正有理数时,有求导公式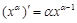 .
.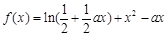 (
(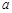 为常数,
为常数,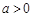 ).
).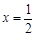 是函数
是函数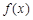 的一个极值点,求
的一个极值点,求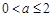 时,
时,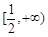 上是增函数;
上是增函数;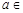 (1,2),总存在
(1,2),总存在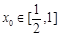 ,使不等式
,使不等式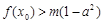 成立,求实数
成立,求实数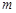 的取范围.
的取范围.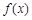 是定义在
是定义在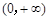 上的非负可导函数,且满足
上的非负可导函数,且满足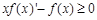 ,对任意正数m,n若
,对任意正数m,n若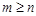 ,则
,则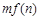 与
与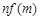 的大小关系是
的大小关系是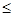 ,
,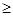 ,或=)
,或=)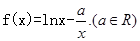
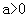 ,试判断函数
,试判断函数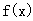 在定义域内的单调性;
在定义域内的单调性;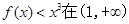 上恒成立,求实数
上恒成立,求实数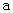 的取值范围。
的取值范围。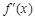 是函数
是函数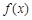 的导函数,
的导函数,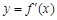 的图象如图1所示,则
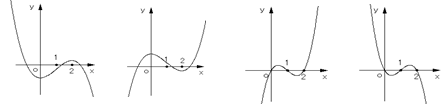
的图象如图1所示,则 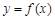 的图象最有可能是下图中的( )
的图象最有可能是下图中的( )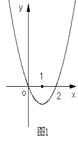
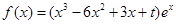 ,
, .
. 依次在
依次在 处取到极值.求
处取到极值.求 的取值范围;
的取值范围; ,使对任意的
,使对任意的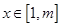 ,不等式
,不等式 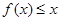 恒成立.求正整数
恒成立.求正整数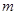 的最大值.
的最大值.