题目内容
11.某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如表所示:| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
参考数据公式:①独立性检验临界值表
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 015. | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6356. | 7.879 | 10.828 |
| A. | 99.9% | B. | 99.5% | C. | 97.5% | D. | 95% |
分析 根据题意,列出2×2列联表,求出观测值K2,根据观测值对应的数值得出结论.
解答 解:根据题意,列出2×2列联表,如下;
| 物理优秀 | 物理不优秀 | 合计 | |
| 数学优秀 | 5 | 1 | 6 |
| 数学不优秀 | 2 | 12 | 14 |
| 合计 | 7 | 13 | 20 |
因为观测值对应的数值为0.005,
所以有99.5%的把握认为学生的数学成绩与物理成绩之间有关系.
故选:B
点评 本题考查了列出2×2列联表以及独立性检验的应用问题,是基础题目.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
3.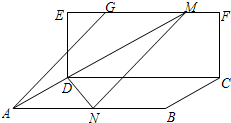 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-C的平面角的取值范围为( )
 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-C的平面角的取值范围为( )
| A. | [30°,45°] | B. | [45°,60°] | C. | [30°,90°) | D. | [60°,90°) |
4.若A,B,C是函数f(x)=ex+x图象上横坐标成等差数列的三个点,给出以下判断:①△ABC可能是直角三角形;②△ABC一定是钝角三角形;③△ABC可能是等腰三角形;④△ABC一定不是等腰三角形.其中,正确的判断是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
20.已知函数f(x)对?x∈R都有f(x)=f(4-x),且其导函数f′(x)满足当x≠2时,(x-2)f′(x)>0,则当2<a<4时,有( )
| A. | f(2a)<f(2)<f(log2a) | B. | f(2)<f(2a)<f(log2a) | C. | f(log2a)<f(2a)<f(2) | D. | f(2)<f(log2a)<f(2a) |
19.在平面直角坐标系xOy中,已知点A(2,0),直线l:x+y-5=0,点B(x,y)是圆C:x2+2x+y2-1=0上的动点,AD⊥l,BE⊥l,垂足分别为D,E,则线段DE的最大值是( )
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{5\sqrt{2}}}{2}$ |