题目内容
已知函数f（x）=sinx+
cosx的图象关于直线x=a对称，则最小正实数a的值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：两角和与差的正弦函数
专题：三角函数的图像与性质
分析：利用三角恒等变换可得f（x）=2sin（x+
），利用正弦函数的对称性即可求得答案．
| π |
| 3 |
解答：
解：∵f（x）=sinx+
cosx=2（
sinx+
cosx）=2sin（x+
），
∴其对称轴方程由x+
=kπ+
，k∈Z．
得：x=kπ+
，k∈Z．又函数f（x）=sinx+
cosx的图象关于直线x=a对称，
∴a=kπ+
，k∈Z．
当k=0时，最小正实数a的值为
．
故选：A．
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∴其对称轴方程由x+
| π |
| 3 |
| π |
| 2 |
得：x=kπ+
| π |
| 6 |
| 3 |
∴a=kπ+
| π |
| 6 |
当k=0时，最小正实数a的值为
| π |
| 6 |
故选：A．
点评：本题考查正弦函数的对称性，求得a=kπ+
（k∈Z）是关键，属于中档题．
| π |
| 6 |
练习册系列答案
相关题目
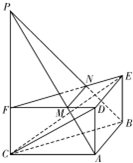如图，在正三棱柱ABC-DEF中，AB=2，AD=1．P是CF的沿长线上一点，FP=t．过A，B，P三点的平面交FD于M，交FE于N．