题目内容
2．已知集合A={x|x2-x+a=0}的子集有4个，则实数a的取值范围为（ ）| A． | $（{\frac{1}{4}，+∞}）$ | B． | $[{\frac{1}{4}，+∞}）$ | C． | $（{-∞，\frac{1}{4}}）$ | D． | $（{-∞，\frac{1}{4}}]$ |
分析 根据集合A子集的个数求出A有2个元素，结合二次函数的性质求出a的范围即可．
解答 解：集合A={x|x2-x+a=0}的子集有4个，
则集合A有2个元素，
故方程x2-x+a=0有2 个不相等的实数根，
故△=1-4a＞0，解得：a＜$\frac{1}{4}$，
故选：C．
点评 本题考查了二次函数的性质，考查集合的子集的个数问题，是一道基础题．
练习册系列答案
相关题目
12．函数$y=\sqrt{x}-1$的值域是（ ）
| A． | [0，+∞） | B． | （0，+∞） | C． | [-1，+∞） | D． | （-1，+∞） |
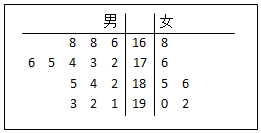某公司从大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩如茎叶图所示（单位：分）．公司规定：成绩在180分以上者到甲部门工作，180分以下者到乙部门工作，另外只有成绩高于180分的男生才能担任助理工作．
10．已知△ABC，$A（{1，1}），B（{1，3}），C（{1+\sqrt{3}，2}）$，若点（x，y）在三角形内部（不包含边界），则z=-2x+y的取值范围是（ ）
| A． | $（{-\sqrt{3}，-1}）$ | B． | （-1，1） | C． | $（{-2\sqrt{3}，1}）$ | D． | $（{-1，\sqrt{3}}）$ |