题目内容
已知在(
-
)n的展开式中,第5项与第3项的二项式系数之比为14:3.
(1)求展开式的常数项;
(2)求(1-x)3+(1-x)4+…+(1-x)10展开式中x2项的系数.
| x |
| 2 |
| x2 |
(1)求展开式的常数项;
(2)求(1-x)3+(1-x)4+…+(1-x)10展开式中x2项的系数.
考点:二项式定理
专题:二项式定理
分析:(1)由条件解方程求得n=10,在二项展开式中的通项公式中,令x的幂指数等于零,求得r的值,可得展开式的常数项.
(2)(1-x)3+(1-x)4+…+(1-x)10展开式中x2项的系数为
+
+…+
,再利用二项式系数的性质花简求得结果.
(2)(1-x)3+(1-x)4+…+(1-x)10展开式中x2项的系数为
| C | 2 3 |
| C | 2 4 |
| C | 2 10 |
解答:
解:(1)由题意知
=
,即
=
,
化简得n2-5n-50=0,解得n=10,或n=-5(舍).
二项展开式中的通项公式为 Tr+1=
(
)10-r(-
)r=
(-2)rx
-2r,
令
-2r=0,解得r=2,故常数项为第三项为
(-2)2=180.
(2)(1-x)3+(1-x)4+…+(1-x)10展开式中x2项的系数为
+
+…+
=
+
+
+…+
-
=
+
+…
-
=
-1=164.
| ||
|
| 14 |
| 3 |
| ||
|
| 14 |
| 3 |
化简得n2-5n-50=0,解得n=10,或n=-5(舍).
二项展开式中的通项公式为 Tr+1=
| C | r 10 |
| x |
| 2 |
| x2 |
| C | r 10 |
| 10-r |
| 2 |
令
| 10-r |
| 2 |
| C | 2 10 |
(2)(1-x)3+(1-x)4+…+(1-x)10展开式中x2项的系数为
| C | 2 3 |
| C | 2 4 |
| C | 2 10 |
=
| C | 3 3 |
| C | 2 3 |
| C | 2 4 |
| C | 2 10 |
| C | 3 3 |
| C | 3 4 |
| C | 2 4 |
| C | 2 10 |
| C | 3 3 |
| C | 3 11 |
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
已知p:“tanαtanβ=1”,q:“cos(α+β)=0”,那么p是q的( )条件.
| A、充要 |
| B、既不充分,也不必要 |
| C、必要不充分 |
| D、充分不必要 |
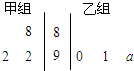 如图所示茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩,乙组记录中有一个数字模糊,无法确认.假设这个数字具有随机性,并在图中以a表示.
如图所示茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩,乙组记录中有一个数字模糊,无法确认.假设这个数字具有随机性,并在图中以a表示. 广州恒大队中6名主力队员在亚冠最后三场比赛中传出的威胁球个数如下表所示:
广州恒大队中6名主力队员在亚冠最后三场比赛中传出的威胁球个数如下表所示: