题目内容

5．若点（-4，-2）在直线2x-y+m=0的下方，则m的取值范围是m＞6．

分析 根据点与不等式的关系进行转化求解即可．

解答 解：∵点（-4，-2）在直线2x-y+m=0的下方，
∴点（-4，-2）满足不等式2x-y+m＞0，
即-8+2+m＞0，得m＞6，
故答案为：m＞6．

点评 本题主要考查二元一次不等式表示平面区域，根据点与平面区域的关系转化为不等式关系是解决本题的关键．

练习册系列答案
相关题目
15．袋子中有大小、质地相同的红球、黑球各一个，现有放回地随机摸取3次，每次摸取一个球，若摸出红球，得10分，摸出黑球，得5分，则3次摸球所得总分至少是25分的概率是$\frac{1}{2}$．
16．已知函数f（x）=sin（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，且函数y=f（x）图象的两相邻对称轴间的距离为$\frac{π}{2}$．
（1）求f（$\frac{π}{8}$）的值；
（2）函数h（x）=af$（\frac{x}{2}）-{sin^2}$x，x∈[$\frac{π}{6}，\frac{2π}{3}$]，有最小值为-1，求a的值和函数h（x）的最大值．
13．设xy＞0，则$（{x^2}+\frac{4}{y^2}）（{y^2}+\frac{1}{x^2}）$的最小值为（　　）
A．-9B．9C．10D．0
20．已知数列{an}满足${a_n}•{a_{n+1}}=\frac{n}{n+2}，（n∈{N^*}）$，${a_1}=\frac{1}{2}$．
（1）求a2，a3，a4值；
（2）归纳猜想数列{an}的通项公式，并用数学归纳法证明．
10．已知x＞1，则函数$y=\frac{{{x^2}+x+1}}{x-1}$的最小值为$3+2\sqrt{3}$．
17．已知数列{an}中，an=-3n+4，等比数列{bn}的公比q满足q=an-an-1（n≥2）且b1=a1，则满足$\frac{1}{{|{b_1}|}}+\frac{1}{{|{b_2}|}}+…+\frac{1}{{|{b_n}|}}＜\frac{121}{81}$成立的n的最大值为（　　）
A．3B．4C．5D．6
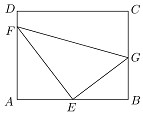14．如图，某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道（直角△EFG，E是直角顶点）来处理污水，管道越长，污水净化效果越好，设计要求管道的接口E是AB的中点，F、G分别落在AD、BC上，且AB=20m，$AD=10\sqrt{3}m$，设∠GEB=θ．
（1）试将污水管道的长度l表示成θ的函数，并写出定义域；
（2）当θ为何值时，污水净化效果最好，并求此时管道的长度．
15．若直线y=2x上存在点（x，y）满足约束条件$\left\{\begin{array}{l}{x+y+6＞0}\\{2x-y+8≥0}\\{x≤m}\end{array}\right.$，则实数m的取值范围是（　　）
A．（-2，+∞）B．[-2，+∞）C．（-∞，-2）D．（-∞，-2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网