题目内容
3.圆x2+y2-4x-4y=0上的点到直线x+y-6=0的最大距离和最小距离的差是( )| A. | $\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $4\sqrt{2}$ |
分析 求出圆心和半径,再求圆心到直线的距离,结合半径,求其结果.
解答 解:圆x2+y2-4x-4y=0的圆心(2,2),半径是2$\sqrt{2}$,
圆心到直线x+y-6=0的距离:d=$\frac{|2+2-6|}{\sqrt{2}}$=$\sqrt{2}$<2$\sqrt{2}$
∴圆x2+y2-4x-4y=0上的点到直线x+y-6=0的最大距离和最小距离的差是3$\sqrt{2}$-0=3$\sqrt{2}$.
故选B.
点评 本题考查点到直线的距离公式,圆的一般方程,是中档题.

练习册系列答案
相关题目
16. 如图是一个四棱锥的三视图,则该几何体的体积为( )
如图是一个四棱锥的三视图,则该几何体的体积为( )
 如图是一个四棱锥的三视图,则该几何体的体积为( )
如图是一个四棱锥的三视图,则该几何体的体积为( )| A. | 8 | B. | 9 | C. | 12 | D. | 16 |
12.已知集合A={x|(x+3)(x-1)≤0},B={x|y=lg(x2-x-2)},则A∩(CRB)=( )
| A. | [-3,-1) | B. | [-3,-1] | C. | [-1,1] | D. | (-1,1] |
18.已知集合A={-2,-1,0,1,2,3},集合B={x|-2≤x<2},则集合A∩B=( )
| A. | {x|-2≤x<2} | B. | {x|-2≤x≤1} | C. | {-2,-1,0,1,2} | D. | {-2,-1,0,1} |
8.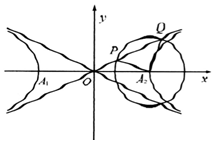 如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
 如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
12.已知函数$f(x)=2-\frac{3}{x}$,若g(x)=f(x)-m为奇函数,则实数m的值为( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
12.已知a∈($\frac{π}{2}$,π),sinα=$\frac{3}{5}$,则tan(α+$\frac{π}{4}$)=( )
| A. | $-\frac{1}{7}$ | B. | 7 | C. | $\frac{1}{7}$ | D. | -7 |