题目内容
13.已知函数f(x)=2sinxcosx-$\sqrt{3}$(cos2x-sin2x).(1)求f(x)的最小正周期;
(2)若f(x0)=$\sqrt{3}$,且x0∈[$\frac{π}{4}$,$\frac{π}{2}$],求x0的值.
分析 (1)利用三角函数的恒等变换、正弦函数的周期性求得f(x)的最小正周期.
(2)由题意利用f(x0)=$\sqrt{3}$,且x0∈[$\frac{π}{4}$,$\frac{π}{2}$],求得x0的值.
解答 解:(1)∵函数f(x)=2sinxcosx-$\sqrt{3}$(cos2x-sin2x)=sin2x-$\sqrt{3}$cos2x=2sin(2x-$\frac{π}{3}$),
∴函数f(x)的最小正周期为$\frac{2π}{2}$=π.
(2)若f(x0)=2sin(2x0-$\frac{π}{3}$)=$\sqrt{3}$,且x0∈[$\frac{π}{4}$,$\frac{π}{2}$],则 2x0-$\frac{π}{3}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],
∴2x0-$\frac{π}{3}$=$\frac{π}{3}$,或 2x0-$\frac{π}{3}$=$\frac{2π}{3}$,∴x0 =$\frac{π}{3}$,或 x0 =$\frac{π}{2}$.
点评 本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,根据三角函数的值求角,属于中档题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
3.已知梯形ABCD中,∠ABC=∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,P是DC的中点,则|$\overrightarrow{PA}$+2$\overrightarrow{PB}$|=( )
| A. | $\frac{\sqrt{82}}{2}$ | B. | 2$\sqrt{5}$ | C. | 4 | D. | 5 |
2.已知$\overrightarrow a=(1\;,\;3)$,$\overrightarrow b=(-2\;,\;5)$,则$3\overrightarrow a-2\overrightarrow b$=( )
| A. | (2,7) | B. | (13,-7) | C. | (7,-1) | D. | (-1,-1) |
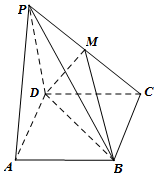 如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,且△PAD是边长为2的等边三角形,$PC=\sqrt{13}$,点M是PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,且△PAD是边长为2的等边三角形,$PC=\sqrt{13}$,点M是PC的中点.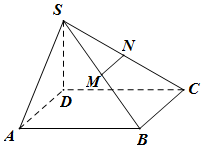 已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.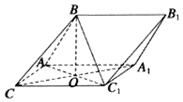 如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.
如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.