题目内容
已知点P(-3,2)在抛物线C:y2=2px(p>0)的准线上,过点P的直线与抛物线C相切于A,B两点,则直线AB的斜率为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、3 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先,求出准线方程x=-3,再求出p,从而得到抛物线方程,写出第一象限和位于第四象限的抛物线方程,分别设出切点,并求导,得到相应切点A、B的坐标,然后再由两点的斜率公式求出BF的斜率.
解答:
解:∵点P(-3,2)在抛物线C:y2=2px(p>0)的准线上,
∴抛物线的准线方程为:x=-
,
∴-
=-3,
∴p=6,
∴y2=12x,
抛物线C:y2=12x,在第一象限的方程为y=2
,
设切点A(m,n),则n=2
,
由导数,得 y′=2
×
=
,
∴在切点A处的斜率为
,
∴直线PA的方程为:y-n=
(x-m).
将点(-3,2)代人,得到
2-n=
(-3-m) ①,
n=2
②,
∴
,
∴A(
,2+2
),
同理,可以设切点B(a,b),得到在该点处的斜率为-
,
∴直线PB的方程为:y-b=-
(x-a).
将点(-3,2)代人,得到
2-b=-
(-3-a) ③
b=-2
④
解得
,
∴B(
,2-2
),
∴直线AB的斜率为:
=3,
故选:D.
∴抛物线的准线方程为:x=-
| p |
| 2 |
∴-
| p |
| 2 |
∴p=6,
∴y2=12x,
抛物线C:y2=12x,在第一象限的方程为y=2
| 3 |
| x |
设切点A(m,n),则n=2
| 3 |
| m |
由导数,得 y′=2
| 3 |
| 1 |
| 2 |
| 1 | ||
|
| ||
|
∴在切点A处的斜率为
| ||
|
∴直线PA的方程为:y-n=
| ||
|
将点(-3,2)代人,得到
2-n=
| ||
|
n=2
| 3 |
| m |
∴
|
∴A(
11+2
| ||
| 3 |
| 10 |
同理,可以设切点B(a,b),得到在该点处的斜率为-
| ||
|
∴直线PB的方程为:y-b=-
| ||
|
将点(-3,2)代人,得到
2-b=-
| ||
|
b=-2
| 3 |
| a |
解得
|
∴B(
11-2
| ||
| 3 |
| 10 |
∴直线AB的斜率为:
(2+2
| ||||||||
|
故选:D.
点评:本题重点考查了切线方程、导数的几何意义、斜率公式、直线与抛物线的位置关系等知识,属于中档题.重点考查运算能力.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
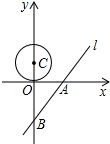 如图所示,已知直线l的解析式是y=
如图所示,已知直线l的解析式是y=