题目内容
(本小题满分12分)设函数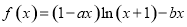 ,其中
,其中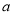 和
和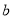 是实数,曲线
是实数,曲线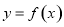 恒与
恒与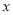 轴相切于坐标原点.
轴相切于坐标原点.
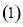 求常数
求常数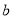 的值;
的值;
 当
当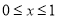 时,关于
时,关于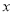 的不等式
的不等式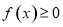 恒成立,求实数
恒成立,求实数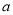 的取值范围;
的取值范围;
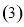 求证:
求证: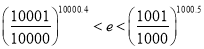 .
.
(1) 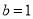 ;(2)
;(2) 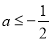 ;(3) 详见解析
;(3) 详见解析
【解析】
试题分析:(1)根据题中条件:曲线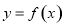 恒与
恒与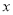 轴相切于坐标原点,可见有:
轴相切于坐标原点,可见有: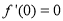 ,即可对函数
,即可对函数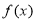 进行求导得:
进行求导得: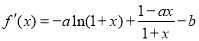 ,根据条件知
,根据条件知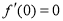 ,可求得
,可求得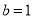 ;(2) 由(1)得
;(2) 由(1)得 ,
,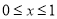 ,观察其特点对其求导可得:
,观察其特点对其求导可得: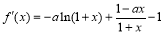 ,观察所得导函数的结构特征,再次对其进行求导得:
,观察所得导函数的结构特征,再次对其进行求导得: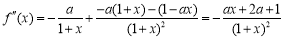 ,其中含有a,对其进行分类讨论:① 当
,其中含有a,对其进行分类讨论:① 当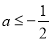 时,由于
时,由于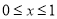 ,有
,有 ,于是
,于是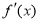 在
在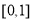 上单调递增,从而
上单调递增,从而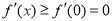 ,因此
,因此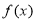 在
在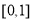 上单调递增,即
上单调递增,即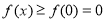 而且仅有
而且仅有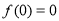 ;②当
;②当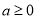 时,由于
时,由于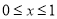 ,有
,有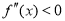 ,于是
,于是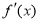 在
在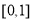 上单调递减,从而
上单调递减,从而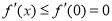 ,因此
,因此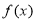 在
在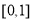 上单调递减,即
上单调递减,即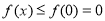 而且仅有
而且仅有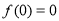 ;③当
;③当 时,令
时,令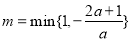 ,当
,当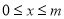 时,
时,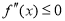 ,于是
,于是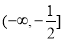 ;(3) 对要证明的不等式等价变形如下:
;(3) 对要证明的不等式等价变形如下: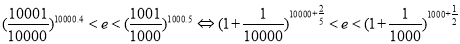
所以可以考虑证明:对于任意的正整数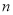 ,不等式
,不等式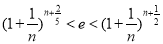 恒成立. 并且继续作如下等价变形
恒成立. 并且继续作如下等价变形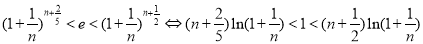 ,可联想到题中函数相当于(2)中
,可联想到题中函数相当于(2)中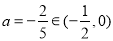 ,
,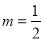 情形,有
情形,有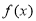 在
在 上单调递减,即
上单调递减,即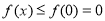 而且仅有
而且仅有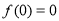 ,可取
,可取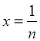 ,当
,当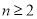 时,
时,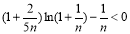 成立;当
成立;当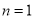 时,
时,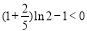 . 从而对于任意正整数
. 从而对于任意正整数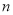 都有
都有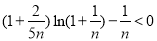 成立;对于相当于(2)中
成立;对于相当于(2)中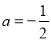 情形,对于任意
情形,对于任意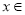
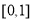 ,恒有
,恒有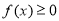 而且仅有
而且仅有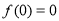 . 取
. 取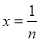 ,得:对于任意正整数
,得:对于任意正整数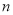 都有
都有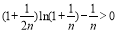 成立,因此对于任意正整数
成立,因此对于任意正整数 ,不等式
,不等式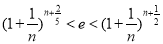 恒成立,这样依据不等式
恒成立,这样依据不等式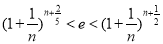 ,再令
,再令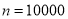 利用左边,令
利用左边,令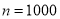 利用右边,即可得到
利用右边,即可得到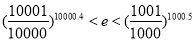 成立.
成立.
试题解析:(1)在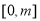 上单调递减,从而
上单调递减,从而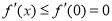 ,因此
,因此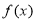 在
在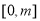 上单调递减,
上单调递减,
即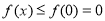 而且仅有
而且仅有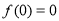 .
.
综上可知,所求实数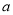 的取值范围是(1) 对
的取值范围是(1) 对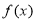 求导得:
求导得: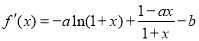 ,根据条件知
,根据条件知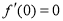 ,所以
,所以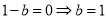 . (3分)
. (3分)
(2) 由(1)得 ,
,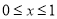

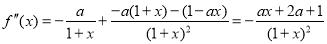 .
.
① 当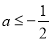 时,由于
时,由于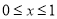 ,有
,有 ,于是
,于是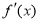 在
在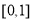 上单调递增,从而
上单调递增,从而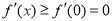 ,因此
,因此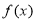 在
在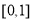 上单调递增,即
上单调递增,即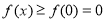 而且仅有
而且仅有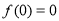 ;
;
②当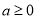 时,由于
时,由于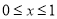 ,有
,有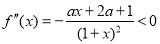 ,于是
,于是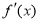 在
在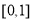 上单调递减,从而
上单调递减,从而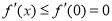 ,因此
,因此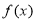 在
在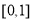 上单调递减,即
上单调递减,即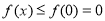 而且仅有
而且仅有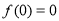 ;
;
③当 时,令
时,令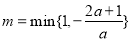 ,当
,当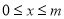 时,
时, ,于是
,于是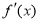
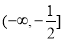 . (8分)
. (8分)
(3) 对要证明的不等式等价变形如下:
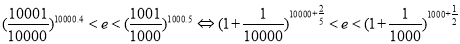
所以可以考虑证明:对于任意的正整数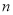 ,不等式
,不等式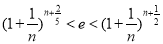 恒成立. 并且继续作如下等价变形
恒成立. 并且继续作如下等价变形
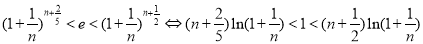

对于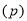 相当于(2)中
相当于(2)中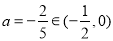 ,
,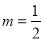 情形,有
情形,有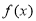 在
在 上单调递减,即
上单调递减,即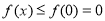 而且仅有
而且仅有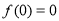 .
.
取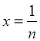 ,当
,当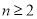 时,
时,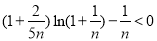 成立;
成立;
当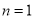 时,
时,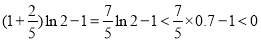 .
.
从而对于任意正整数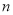 都有
都有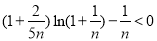 成立.
成立.
对于 相当于(2)中
相当于(2)中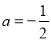 情形,对于任意
情形,对于任意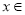
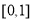 ,恒有
,恒有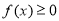 而且仅有
而且仅有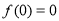 . 取
. 取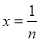 ,得:对于任意正整数
,得:对于任意正整数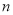 都有
都有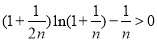 成立.
成立.
因此对于任意正整数 ,不等式
,不等式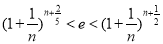 恒成立.
恒成立.
这样依据不等式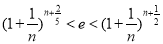 ,再令
,再令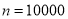 利用左边,令
利用左边,令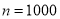 利用右边,即可得到
利用右边,即可得到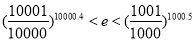 成立. (12分)
成立. (12分)
考点:1.导数来描述原函数的单调性;2. 导数来描述原函数的极值;3.函数零点

 ,则
,则 ( )
( ) B.
B. C.
C. D.(3, 4)
D.(3, 4) 的终边过点
的终边过点 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,若其图象是由
,若其图象是由 图象向左平移
图象向左平移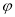 (
( )个单位得到,则
)个单位得到,则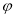 的最小值为( )
的最小值为( )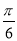 B.
B. C.
C.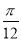 D.
D.
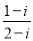 对应的点位于( )
对应的点位于( ) 为偶函数且
为偶函数且 ,又
,又 ,函数
,函数 ,若
,若 恰好有4个零点,则
恰好有4个零点,则 的取值范围是 .
的取值范围是 . ,若将其图象向右平移
,若将其图象向右平移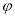 (
(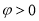 )个单位后所得的图象关于原点对称,则
)个单位后所得的图象关于原点对称,则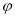 的最小值为( )
的最小值为( )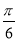 B.
B.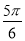 C.
C.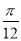 D.
D.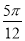

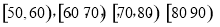
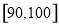 的分组作出频率分布直方图,并作出茎叶图(图中仅列出来
的分组作出频率分布直方图,并作出茎叶图(图中仅列出来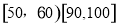 这两组的数据).
这两组的数据).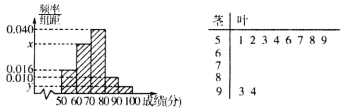
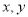 ;
;