题目内容
(本小题满分12分)
某中学举行了一次“社会主义核心价值观知识竞赛”活动,为了解本次竞赛中学生成绩情况,从全体学生中随机抽取了部分学生的分数(得分取整数且不低于50分,满分100分),作为样本(样本容量为n)进行统计.按照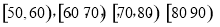
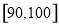 的分组作出频率分布直方图,并作出茎叶图(图中仅列出来
的分组作出频率分布直方图,并作出茎叶图(图中仅列出来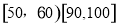 这两组的数据).
这两组的数据).
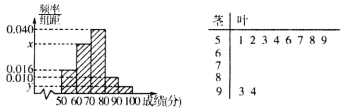
(I)求样本容量n和频率分布直方图中的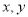 ;
;
(II)在选取的样本中,从样本中竞赛成绩80分以上(含80分)的同学中随机抽取2名同学到市政广场参加社会主义核心价值观知识宣传志愿者活动.求所抽取的2名同学来自不同组的概率.
(Ⅰ) ; (Ⅱ)
; (Ⅱ)
【解析】
试题分析:(Ⅰ)首先根据频率分布直方图的相关概念,即可求得样本容量 和频率分布直方图中
和频率分布直方图中 的值;
的值;
(Ⅱ)由题意可知,分数在[80,90)有5人,分别记为 ,分数在[90,100)有2人,分别记为a,b,用列举法求得所有的抽法有21种,而满足条件的有10种,由此求得所求事件的概率.
,分数在[90,100)有2人,分别记为a,b,用列举法求得所有的抽法有21种,而满足条件的有10种,由此求得所求事件的概率.
试题解析:【解析】
(Ⅰ)由题意可知,样本容量 .
.
(Ⅱ)由题意可知,分数在 有5人,分别记为
有5人,分别记为 ,分数在[90,100)有2人,分别记为a,b.从竞赛成绩是80(分)以上(含80分)的同学中随机抽取2名同学有如下种情形:(1,2),(1,3),(1,4),(1,5),(1,a),(1,b),(2,3),(2,4),(2,5),(2,a),(2,b),(3,4),(3,5),(3,a),(3,b),(4,5),(4,a),(4,b),(5,a),(5,b),(a,b)共有21个基本事件;
,分数在[90,100)有2人,分别记为a,b.从竞赛成绩是80(分)以上(含80分)的同学中随机抽取2名同学有如下种情形:(1,2),(1,3),(1,4),(1,5),(1,a),(1,b),(2,3),(2,4),(2,5),(2,a),(2,b),(3,4),(3,5),(3,a),(3,b),(4,5),(4,a),(4,b),(5,a),(5,b),(a,b)共有21个基本事件;
其中符合“抽取的2名同学来自不同组”的基本事件有(1,a),(1,b),(2,a),(2,b),(3,a),(3,b),(4,a),(4,b),(5,a),(5,b),共10个,所以抽取的2名同学来自不同组的概率 .
.
考点:1.列举法计算基本事件数及事件发生的概率;2.频率分布直方图.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案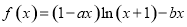 ,其中
,其中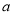 和
和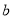 是实数,曲线
是实数,曲线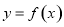 恒与
恒与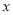 轴相切于坐标原点.
轴相切于坐标原点.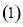 求常数
求常数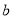 的值;
的值; 当
当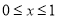 时,关于
时,关于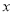 的不等式
的不等式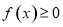 恒成立,求实数
恒成立,求实数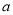 的取值范围;
的取值范围; 求证:
求证: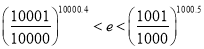 .
. 是纯虚数,则实数m的值为( )
是纯虚数,则实数m的值为( ) (D)
(D)
 的反函数为
的反函数为 ,如果函数
,如果函数 ,那么函数
,那么函数 的图像一定过点 .
的图像一定过点 . 
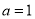 时,求函数
时,求函数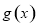 的单调区间;
的单调区间;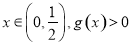 恒成立,求实数
恒成立,求实数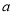 的最小值;
的最小值;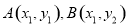 是函数
是函数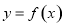 图象上任意不同两点,线段AB中点为C
图象上任意不同两点,线段AB中点为C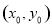 ,直线AB的斜率为k.证明:
,直线AB的斜率为k.证明: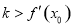 .
. ,
, __________.
__________. 的直线与圆
的直线与圆 有公共点,则该直线的倾斜角的取值范围是( )
有公共点,则该直线的倾斜角的取值范围是( ) B.
B. 
 D.
D. 
 为纯虚数,则实数
为纯虚数,则实数
 B.
B.  C.2 D.
C.2 D. 
 和圆
和圆 的位置关系为
的位置关系为