题目内容
已知实数x、y满足
,且μ=ax+2y(a>0且a≠1)的最大值为4,则a= .
|
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:画出x,y满足
的可行域,令z=x+2y,则由图象求出z的最值,再讨论a>1,0<a<1,由指数函数的单调性即可求出a的值.
|
解答:
解: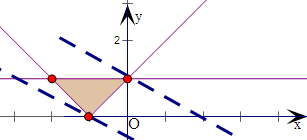 画出x,y满足
画出x,y满足
的可行域,如图三角形区域,
令z=x+2y,则由图象可知过(-1,0),
z取最小值-1,
过(0,1),z取最大值2.
故μ=ax+2y(a>0且a≠1),当a>1时,
μ=a2最大且为4,则a=2;
当0<a<1时,μ=a-1最大,且为4,则a=
.
故a=2或
.
故答案为:2或
.
 画出x,y满足
画出x,y满足
|
令z=x+2y,则由图象可知过(-1,0),
z取最小值-1,
过(0,1),z取最大值2.
故μ=ax+2y(a>0且a≠1),当a>1时,
μ=a2最大且为4,则a=2;
当0<a<1时,μ=a-1最大,且为4,则a=
| 1 |
| 4 |
故a=2或
| 1 |
| 4 |
故答案为:2或
| 1 |
| 4 |
点评:本题考查分段函数的图象和运用,考查线性规划的应用,指数函数的单调性及应用,属于中档题.

练习册系列答案
相关题目
对于函数y=f(x),以下说法正确的有( )
①y是x的函数;②对于不同的x值,y值也不同;③函数是一种对应,是多对一或一对一,不是一对多.
①y是x的函数;②对于不同的x值,y值也不同;③函数是一种对应,是多对一或一对一,不是一对多.
| A、①② | B、①③ | C、②③ | D、①②③ |
 如图,AB是圆O直径,CD⊥AB,过点C的切线与BA的延长线相交于点P.若AB=6,CD=2
如图,AB是圆O直径,CD⊥AB,过点C的切线与BA的延长线相交于点P.若AB=6,CD=2