题目内容
17.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4)=f(x),且当x∈[-2,0]时,f(x)=($\frac{1}{3}$)x-6.若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则实数a的取值范围是$({\root{3}{4},2})$.分析 由f(x+4)=f(x),推出函数的周期是4,根据函数f(x)是偶函数,得到函数f(x)在一个周期内的图象,利用方程和函数之间的关系,转化为两个函数的交点个数问题,利用数形结合确定满足的条件即可得到结论.)
解答 解:由f(x+4)=f(x),即函数f(x)的周期为4,
∵当x∈[-2,0]时,f(x)=($\frac{1}{3}$)x-6.
∴若x∈[0,2],则-x∈[-2,0],
则f(-x)=($\frac{1}{3}$)-x-6=3x-6,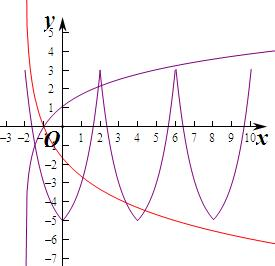
∵f(x)是偶函数,
∴f(-x)=3x-6=f(x),
即f(x)=3x-6,x∈[0,2],
由f(x)-loga(x+2)=0得f(x)=loga(x+2),
作出函数f(x)的图象如图:当a>1时,要使方程f(x)-loga(x+2)=0恰有3个不同的实数根,
则等价为函数f(x)与g(x)=loga(x+2)有3个不同的交点,
则满足$\left\{\begin{array}{l}{g(2)<f(2)}\\{g(6)>f(6)}\end{array}\right.$,即$\left\{\begin{array}{l}{lo{g}_{a}4<3}\\{lo{g}_{a}8>3}\end{array}\right.$,
解得$\root{3}{4}<a<2$,
故a的取值范围是$({\root{3}{4},2})$,
故答案为:$({\root{3}{4},2})$.
点评 本题主要考查函数零点的个数判断,利用函数和方程之间的关系转化为两个函数的交点个数问题,利用分段函数的表达式,作出函数f(x)的图象是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
18.已知U=R,函数y=log2(2-x)的定义域为M,N={x|x2-2x<0},则下列结论正确的是( )
| A. | M∩(∁UN)=∅ | B. | M∩N=N | C. | M∪N=U | D. | M⊆(∁UN) |
5.已知不等式ax2+bx+c>0的解集为$\left\{{x|-\frac{1}{3}<x<2}\right\}$,则不等式cx2+bx+a<0的解集为( )
| A. | $\left\{{x|-3<x<\frac{1}{2}}\right\}$ | B. | $\left\{{x|x<-3或x>\frac{1}{2}}\right\}$ | C. | $\left\{{x|-2<x<\frac{1}{3}}\right\}$ | D. | $\left\{{x|x<-2或x>\frac{1}{3}}\right\}$ |
2.函数f(x)=cosωx(ω>0)的图象关于点M($\frac{3π}{4}$,0)对称,且在区间[0,$\frac{π}{2}$]上是单调函数,则ω的值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$或$\frac{1}{2}$ | D. | $\frac{2}{3}$或2 |
9.计算:${∫}_{0}^{1}$x3dx=( )
| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
6.i是虚数单位,复数$\frac{7+i}{3+4i}$=( )
| A. | $\frac{17}{25}$+$\frac{31}{25}$i | B. | -1+i | C. | 1-i | D. | -$\frac{17}{7}$+$\frac{25}{7}$i |