题目内容
从长32cm，宽20cm的矩形薄铁板的四角剪去相等的正方形，做一个无盖的箱子，若使箱子的容积最大，则剪去的正方形边长为（ ）
| A、4cm | B、2cm |
| C、1cm | D、3cm |
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：设剪去的正方形的边长为xcm，（0＜x＜10），箱子的容积V=（32-2x）（20-2x）•x=4（x3-26x2+160x），V′=12（x-4）（x-
），由此利用导数性质能求出若使箱子的容积最大，则剪去的正方形边长为4cm．
| 40 |
| 3 |
解答：
解：设剪去的正方形的边长为xcm，（0＜x＜10），
则做成的无盖的箱子的底是长为（32-2x）cm，宽为（20-2x）cm的矩形，
箱子的高为xcm，
∴箱子的容积V=（32-2x）（20-2x）•x=4（x3-26x2+160x），
V′=12（x-4）（x-
），
当0＜x＜10时，V′=0只有一个解x=4，
在x=4附近，V′是左正右负，
∴V有x=4处取得极大值即为最大值，
∴若使箱子的容积最大，则剪去的正方形边长为4cm．
故选：A．
则做成的无盖的箱子的底是长为（32-2x）cm，宽为（20-2x）cm的矩形，
箱子的高为xcm，
∴箱子的容积V=（32-2x）（20-2x）•x=4（x3-26x2+160x），
V′=12（x-4）（x-
| 40 |
| 3 |
当0＜x＜10时，V′=0只有一个解x=4，
在x=4附近，V′是左正右负，
∴V有x=4处取得极大值即为最大值，
∴若使箱子的容积最大，则剪去的正方形边长为4cm．
故选：A．
点评：本题考查棱柱体积的求法及应用，是中档题，解题时要注意导数性质的合理运用．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
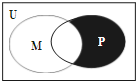设全集U=Z，集合M={1，2}与P={x||x|＜2，x∈Z}关系的韦恩（venn）图如图所示，则阴影部分所示的集合为（ ）| A、{-1，0} |
| B、{-2，-1，0} |
| C、{0，1，2} |
| D、{0，1} |
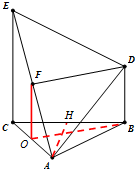如图，在多面体ECABD中，EC⊥平面ABC，DB∥EC，△ABC为正三角形，F为EA的中点，EC=AC=2，BD=1．
已知三角形△ABC的三个顶点分别为A（-1，0），B（1，0），C（0，1）．