题目内容
2.已知α,β为锐角,且$\frac{sinβ}{sinα•cos(α+β)}$=λ,求证:tanβ=$\frac{λtanα}{1+(1+λ{)tan}^{2}α}$.分析 将λ=$\frac{sinβ}{sinα•cos(α+β)}$代入右边式子化简即可.
解答 证明:∵$\frac{sinβ}{sinα•cos(α+β)}$=λ,
∴λtanα=$\frac{sinβ}{sinα•cos(α+β)}$$•\frac{sinα}{cosα}$=$\frac{sinβ}{cosαcos(α+β)}$.
1+(1+λ)tan2α=1+$\frac{si{n}^{2}α}{co{s}^{2}α}$+$\frac{sinβ}{cosαcos(α+β)}$•$\frac{sinα}{cosα}$=$\frac{co{s}^{2}αcos(α+β)+si{n}^{2}αcos(α+β)+sinαsinβ}{co{s}^{2}αcos(α+β)}$=$\frac{cos(α+β)+sinαsinβ}{co{s}^{2}αcos(α+β)}$.
∴$\frac{λtanα}{1+(1+λ{)tan}^{2}α}$=$\frac{sinβ}{cosαcos(α+β)}$•$\frac{co{s}^{2}αcos(α+β)}{cos(α+β)+sinαsinβ}$=$\frac{cosαsinβ}{cosαcosβ}$=tanβ.
∴tanβ=$\frac{λtanα}{1+(1+λ{)tan}^{2}α}$.
点评 本题考查了三角函数的恒等变换,熟练掌握三角公式是解题关键.

练习册系列答案
相关题目
13.若集合A={x|x2-4x<0},B={y|y=2x-5,x∈A},则A∩B等于( )
| A. | ∅ | B. | (0,3) | C. | (-5,4) | D. | (0,4) |
10.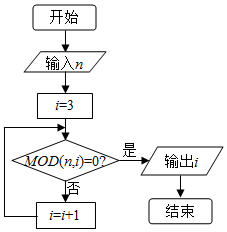 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )
 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
17.运行如图程序,若随机输人一个x值,则输出的结果不可能是( )


| A. | -3 | B. | 0 | C. | 0.5 | D. | 2 |
12.函数y=log2(x+1)+1(x>1)的反函数为( )
| A. | y=2x-1+1(x>2) | B. | y=2x+1+1(x>0) | C. | y=2x-1-1(x>2) | D. | y=2x+1-1(x>0) |