题目内容
 如图,在三棱柱ABC-A1B1C1中,底面△ABC为直角三角形,∠ACB=
如图,在三棱柱ABC-A1B1C1中,底面△ABC为直角三角形,∠ACB=| π |
| 2 |
(1)若T是△ABC1的重心,求直线A1T与平面ABC1所成角;
(2)是否存在点T,使TB1=TC且平面TA1C1⊥平面ACC1A1,若存在,求出线段TC的长度,若不存在,说明理由.
考点:二面角的平面角及求法,平面与平面垂直的性质
专题:空间位置关系与距离
分析:(1)以CB、CA分别为x,y轴,过C作直线Cz∥BC1,以Cz为z轴建立空间坐标系,求出直线A1T的方向向量和平面ABC1的法向量,代入向量夹角公式,可得直线A1T与平面ABC1所成角;
(2)T在面ABC1内,
=
+
=
+m
+n
,由TB1=TC得,-2m+4n=-1…①;求出面CAA1C1法向量
和面TA1C1法向量
,由平面TA1C1⊥平面ACC1A1,得:m=n+1…②,解方程组求出m,n的值,进而可得TC的长度.
(2)T在面ABC1内,
| CT |
| CB |
| BT |
| CB |
| BC1 |
| BA |
| n |
| i |
解答:
 解:如图以CB、CA分别为x,y轴,过C作直线Cz∥BC1,以Cz为z轴建立空间坐标系,
解:如图以CB、CA分别为x,y轴,过C作直线Cz∥BC1,以Cz为z轴建立空间坐标系,
则B(3,0,0),C(0,0,0),A(0,3,3),C1(3,0,3),
∵
=
+
=(6,0,3),
∴B1(6,0,3),
∵
=
+
=(3,3,3),
∴A1(3,3,3),
(1)∵T是△ABC1重心,
∴T(2,1,1),
∴
=(1,2,2),
设面ABC1的法向量为
=(x,y,z),
由
=(3,-3,0),及
得:
令x=1,则
=(1,1,0),
设直线A1T与平面ABC1所成角为θ,
则cosθ=
=
=
,
故θ=
,
故直线A1T与平面ABC1所成角为
.
(2)T在面ABC1内,
=
+
=
+m
+n
=(3-3n,3n,3m),
即T(3-3n,3n,3m).由TB1=TC得:
(3-3n)2+(3n)2+(3m)2=(3n+3)2+(3n)2+(3m-3)2,
即-2m+4n=-1…①
设面CAA1C1法向量为
=(a,b,c),由
=(0,3,0),
=(3,0,3)得:
,
取a=1,则
=(1,0,-1),
设面TA1C1法向量为
=(x,y,z),
由
=(0,3,0),
=(-3n,3n,3m-3),得:
取x=m-1,则
=(m-1,0,n),
由平面TA1C1⊥平面ACC1A1,得:
cos<
,
>=
=0,
即m=n+1…②
由①②解得,
n=
,m=
,
∴存在点T(
,
,
)满足条件,此时TC=
.…10分
 解:如图以CB、CA分别为x,y轴,过C作直线Cz∥BC1,以Cz为z轴建立空间坐标系,
解:如图以CB、CA分别为x,y轴,过C作直线Cz∥BC1,以Cz为z轴建立空间坐标系,则B(3,0,0),C(0,0,0),A(0,3,3),C1(3,0,3),
∵
| CB1 |
| CC1 |
| CB |
∴B1(6,0,3),
∵
| CA1 |
| CC1 |
| CA |
∴A1(3,3,3),
(1)∵T是△ABC1重心,
∴T(2,1,1),
∴
. |
| TA1 |
设面ABC1的法向量为
| m |
由
| AB |
|
|
令x=1,则
| m |
设直线A1T与平面ABC1所成角为θ,
则cosθ=
|
| ||||
|
|
| 3 | ||
3×
|
| ||
| 2 |
故θ=
| π |
| 4 |
故直线A1T与平面ABC1所成角为
| π |
| 4 |
(2)T在面ABC1内,
| CT |
| CB |
| BT |
| CB |
| BC1 |
| BA |
即T(3-3n,3n,3m).由TB1=TC得:
(3-3n)2+(3n)2+(3m)2=(3n+3)2+(3n)2+(3m-3)2,
即-2m+4n=-1…①
设面CAA1C1法向量为
| n |
| CA |
| CC1 |
|
取a=1,则
| n |
设面TA1C1法向量为
| i |
由
| C1A1 |
| C1T |
|
取x=m-1,则
| i |
由平面TA1C1⊥平面ACC1A1,得:
cos<
| n |
| i |
| m-1-n | ||||
|
即m=n+1…②
由①②解得,
n=
| 1 |
| 2 |
| 3 |
| 2 |
∴存在点T(
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
3
| ||
| 2 |
点评:本题考查的知识点是平面与平面垂直的性质,二面角的平面角及求法,直线与平面的夹角,其中建立空间直角坐标系,将问题转化为向量夹角问题是解答的关键.

练习册系列答案
相关题目
设f(x)=
,则不等式f(x)≥2的解集为( )
|
| A、(-∞,1]∪[3,+∞) |
| B、(-∞,-1]∪[2,+∞) |
| C、[3,+∞) |
| D、(-∞,-1] |
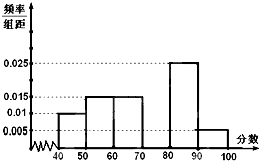 某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: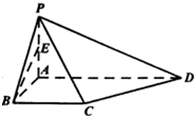 如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.
如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.