题目内容
19.定义域为D的函数f(x)同时满足条件:①常数a,b满足a<b,区间[a,b]⊆D,②使f(x)在[a,b]上的值域为[at,bt](t∈N+),那么我们把f(x)叫做[a,b]上的“t级矩形”函数,函数f(x)=x3是[a,b]上的“2级矩形”函数,则满足条件的常数对(a,b)共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
分析 函数f(x)=x3是[a,b]上的“2级矩阵”函数,即满足条件①常数a,b满足a<b,区间[a,b]⊆D,②使f(x)在[a,b]上的值域为[at,bt],利用函数f(x)=x3是[a,b]上的单调增函数,即可求得满足条件的常数对.
解答 解:由题意,函数f(x)=x3是[a,b]上的“2级矩阵”函数,
即满足条件①常数a,b满足a<b,区间[a,b]⊆D,
②使f(x)在[a,b]上的值域为[at,bt],
∵函数f(x)=x3是[a,b]上的单调增函数,
∴$\left\{\begin{array}{l}{{a}^{3}=2a}\\{{b}^{3}=2b}\end{array}\right.$,∴满足条件的常数对(a,b)为(-$\sqrt{2}$,0),(-$\sqrt{2}$,$\sqrt{2}$),(0,$\sqrt{2}$),
故选:C.
点评 本题考查了新定义型函数的理解和运用能力,函数单调性的应用,转化化归的思想方法.

练习册系列答案
相关题目
10.下列四个结论:
①若p∧q是真命题,则¬p可能是真命题;
②命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0”;
③“a>5且b>-5”是“a+b>0”的充要条件;
④当a<0时,幂函数y=xa在区间(0,+∞)上单调递减.
其中正确结论的个数是( )
①若p∧q是真命题,则¬p可能是真命题;
②命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0”;
③“a>5且b>-5”是“a+b>0”的充要条件;
④当a<0时,幂函数y=xa在区间(0,+∞)上单调递减.
其中正确结论的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
4.若函数y=f(x)的导函数为y=f′(x),且f′(x)=sin2x-$\sqrt{3}$cos2x,则下列说法正确的是( )
| A. | y=f(x)的周期为$\frac{π}{2}$ | B. | y=f(x)在[0,$\frac{π}{6}$]上是减函数 | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)是偶函数 |
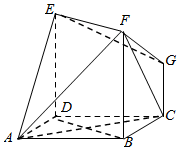 如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.
如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.