题目内容
8.求双曲线2x2-y2=8的实轴长,虚轴长,离心率,渐近线方程,焦点坐标,顶点坐标.分析 把双曲线方程化为标准方程,分别求出a,b,c,由此能求出此双曲线的实轴长,虚轴长,离心率,渐近线方程,焦点坐标,顶点坐标.
解答 解:∵双曲线方程2x2-y2=8,
∴双曲线的标准方程为:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{8}$=1,
∴a=2,b=2$\sqrt{2}$,c=2$\sqrt{3}$
∴该双曲线的实轴长为2a=4,虚轴长为2b=4$\sqrt{2}$,渐近线方程为y=±$\sqrt{2}$x,离心率e=$\frac{c}{a}$=$\sqrt{3}$,焦点坐标($±2\sqrt{3}$,0),顶点坐标(±2,0).
点评 本题考查双曲线的简单性质,是基础题,解题时要把双曲线方程转化为标准方程.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
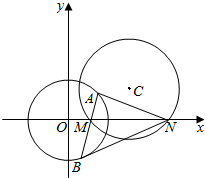 如图,圆C:x2-(1+a)x+y2-ay+a=0.
如图,圆C:x2-(1+a)x+y2-ay+a=0.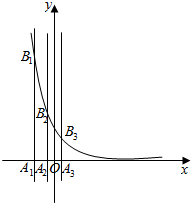 (文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.