题目内容
9.已知数列{an}为等比数列,数列{bn}为等差数列,且a2a3=a5=32,b2+b3=b5=5.(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn,求和Tn=b1S1+b2S2+…+bnSn.
分析 (I)利用等差数列与等比数列的通项公式即可得出;
(II)利用“错位相减法”、等差数列与等比数列的前n项和公式即可得出.
解答 解:(I)设等比数列{an}的公比为q,等差数列{bn}的公差为d,
∵a2•a3=a5=32,b2+b3=b5=5.
∴${a}_{1}^{2}$q3=${a}_{1}{q}^{4}$=32,2b1+3d=b1+4d=5,
解得:a1=q=2,b1=d=1.
∴an=2n,bn=1+(n-1)=n.
(II)Sn=$\frac{2({2}^{n}-1)}{2-1}$=2n+1-2.
∴bnSn=n•2n+1-2n.
设数列{n•2n+1}的前n项和为An.
∴An=22+2×23+3×24+…+n•2n+1,
∴2An=23+2×24+…+(n-1)•2n+1+n•2n+2,
∴-An=22+23+…+2n+1-n•2n+2=$\frac{4({2}^{n}-1)}{2-1}$-n•2n+2=(1-n)•2n+2-4,
∴An=(n-1)•2n+2+4,
∴和Tn=b1S1+b2S2+…+bnSn=(n-1)•2n+2+4-$\frac{n(2n+2)}{2}$
=(n-1)•2n+2+4-n2-n.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.若实数x,y满足$\left\{\begin{array}{l}{x-2y≤0}\\{2x-y≥0}\\{x+y≥3}\end{array}\right.$,则下列不等成立的是( )
| A. | x2+y2≥5 | B. | $\frac{y}{x-2}$≥-2 | C. | 2x+y≥5 | D. | |x+3y-1|≥4 |
1.不等式$\frac{5-x}{x-1}≥1$的解集为( )
| A. | (-∞,-3)∪(3,+∞) | B. | (-∞,1)∪(3,+∞) | C. | [1,3] | D. | (1,3] |
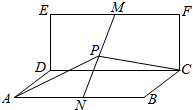 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=2$\sqrt{2}$,DE=2,AB=4,点M,N分别为线段EF,AB上的动点,点P为MN的中点,则PA+PC的最小值为2$\sqrt{7}$.
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=2$\sqrt{2}$,DE=2,AB=4,点M,N分别为线段EF,AB上的动点,点P为MN的中点,则PA+PC的最小值为2$\sqrt{7}$.