��Ŀ����
8����OΪ��ABC��һ�㣬������$\overrightarrow{OA}+\overrightarrow{OB}+4\overrightarrow{OC}=\overrightarrow{0}$�����OBC���ABC������ֱ�ΪS1��S2����$\frac{{S}_{1}}{{S}_{2}}$=��������| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{2}$ |
���� �ӳ�OC��D��ʹOD=4OC���ӳ�CO��AB��E������֪��OΪ��DABC���ģ�EΪAB�е㣬�Ƶ���S��AEC=S��BEC��S��BOE=2S��BOC���ɴ�����������
��� 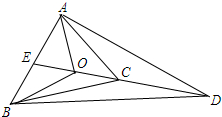 �⣺�ӳ�OC��D��ʹOD=4OC��
�⣺�ӳ�OC��D��ʹOD=4OC��
�ӳ�CO��AB��E��
��OΪ��ABC��һ�㣬������$\overrightarrow{OA}+\overrightarrow{OB}+4\overrightarrow{OC}=\overrightarrow{0}$��
��$\overrightarrow{OD}+\overrightarrow{OA}+\overrightarrow{OB}$=$\overrightarrow{0}$��
��OΪ��DABC���ģ�EΪAB�е㣬
��OD��OE=2��1����OC��OE=1��2����CE��OE=3��2��
��S��AEC=S��BEC��S��BOE=2S��BOC��
�ߡ�OBC���ABC������ֱ�ΪS1��S2��
��$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{6}$��
��ѡ��B��
���� ���⿼�����������������ֵ�������е��⣬����ʱҪ�������⣬ע�����������������ĵ�֪ʶ�ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
3����ʵ��x��y����$\left\{\begin{array}{l}{x-2y��0}\\{2x-y��0}\\{x+y��3}\end{array}\right.$�������в��ȳ������ǣ�������
| A�� | x2+y2��5 | B�� | $\frac{y}{x-2}$��-2 | C�� | 2x+y��5 | D�� | |x+3y-1|��4 |
13��������R�ϵ�ż����f��x�����㣺�������x1��x2�ʣ�-�ޣ�0]��x1��x2������$\frac{{f��{x_2}��-f��{x_1}��}}{{{x_2}-{x_1}}}��0$����f��2��=0����ʽ$\frac{2f��x��+f��-x��}{5��x-1��}$��0�Ľ⼯�ǣ�������
| A�� | ��-�ޣ�-2���ȣ�2��+�ޣ� | B�� | ��-�ޣ�-2���ȣ�1��2�� | C�� | ��-2��1���ȣ�2��+�ޣ� | D�� | ��-2��1���ȣ�1��2�� |