题目内容
16.若f(x)是定义在R上的函数,对任意的实数x都有:f(x+6)≤f(x+2)+4和f(x+4)≥f(x+2)+2,且f(1)=1,则f(2017)=2017.分析 根据f(x+6)≤f(x+2)+4和f(x+4)≥f(x+2)+2,化简出f(x)的关系式,根据f(1)=1,利用赋值法求解,求出周期,即可计算f(2017)的值.
解答 解:对任意的实数x都有:f(x+6)≤f(x+2)+4和f(x+4)≥f(x+2)+2…①,
令x=x-2,则f(x+6)≤f(x+2)+4转化为f(x+4)≤f(x)+4…②.
则f(x+4)≥f(x+2)+2转化为f(x+2)≥f(x)+2…③,
不等式的性质,由①②可得:f(x+2)≤f(x)+2…④..
由③④可得:f(x+2)=f(x)+2.
∵f(1)=1,
∴f(2017)=f(2017-2)+2=f(2017-2×1008)+2×1008=f(1)+2016=2017.
故答案为:2017.
点评 本题主要考查函数值的计算,根据函数的周期性,进行转化是解决本题的关键.

练习册系列答案
相关题目
6.2017年5月14日至15日,中国在北京举办“一带一路”国际合作高峰论坛,与其它60多个成员国共商大计.设S是由不少于4个成员国代表组成的集合,如果S中任意4个代表都至少有1个人与另外3个人认识,那么下列判定正确的是( )
| A. | S中没有人认识S中所有的人 | B. | S中至少有1人认识S中所有的人 | ||
| C. | S中至多有2人不认识S中所有的人 | D. | S中至多有2人认识S中所有的人 |
7.化简$C_n^0-2C_n^1+{2^2}C_n^2+…+{(-1)^n}{2^n}C_n^n$=( )
| A. | 1 | B. | -1 | C. | (-1)n | D. | (-1)n-1 |
11.正整数按如表的规律排列,则第2017行,第2016列的数应为( )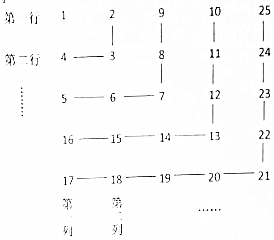

| A. | 20162 | B. | 2016×2017 | C. | 20172 | D. | 2017×2018 |
1.网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )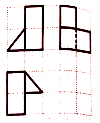

| A. | 2 | B. | 4 | C. | $\frac{2\sqrt{2}}{3}$ | D. | 1+$\frac{2\sqrt{2}}{3}$ |
8.观察下列各式:55=3 125,56=15 625,57=78 125,58=390 625,59=1 953 125,…,则585的末四位数字为( )
| A. | 3125 | B. | 5625 | C. | 8125 | D. | 0625 |
5.执行如图的程序框图,输出S的值是( )


| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |