题目内容
下列几个命题:
①方程x2+(a-3)x+a=0有一个正实根,一个负实根,则a<0;
②函数y=
+
是偶函数,但不是奇函数;
③函数f(x)的定义域是[-2,2],则函数f(x+1)的定义域为[-1,3];
④一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,则m的值不可能是1.
其中真命题的个数是( )
①方程x2+(a-3)x+a=0有一个正实根,一个负实根,则a<0;
②函数y=
| x2-1 |
| 1-x2 |
③函数f(x)的定义域是[-2,2],则函数f(x+1)的定义域为[-1,3];
④一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,则m的值不可能是1.
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:阅读型,数形结合,函数的性质及应用
分析:①运用判别式大于0且两根之积小于0,即可求出a的范围;
②先求函数的定义域,再化简函数,判断函数的奇偶性;
③由函数的定义域的概念,令-2≤x+1≤2,求出x的范围,即为所求函数的定义域;
④画出曲线y=|3-x2|,直线y=a,通过观察,即可得到交点个数.
②先求函数的定义域,再化简函数,判断函数的奇偶性;
③由函数的定义域的概念,令-2≤x+1≤2,求出x的范围,即为所求函数的定义域;
④画出曲线y=|3-x2|,直线y=a,通过观察,即可得到交点个数.
解答:
解:①若方程x2+(a-3)x+a=0有一个正实根,一个负实根,则判别式大于0且两根之积小于0,
即(a-3)2-4a>0且a<0,解得a<0,故①对;
②函数y=
+
的定义域为{-1,1},即y=0,则函数既是偶函数,又是奇函数,故②错;
③函数f(x)的定义域是[-2,2],令-2≤x+1≤2,
则-3≤x≤1,则函数f(x+1)的定义域为[-3,1],故③错;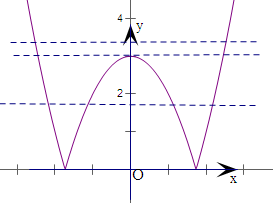
④画出曲线y=|3-x2|,直线y=a,
则曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,m=0,2,3,4,则m的值不可能是1,故④对.
故选:B.
即(a-3)2-4a>0且a<0,解得a<0,故①对;
②函数y=
| x2-1 |
| 1-x2 |
③函数f(x)的定义域是[-2,2],令-2≤x+1≤2,
则-3≤x≤1,则函数f(x+1)的定义域为[-3,1],故③错;

④画出曲线y=|3-x2|,直线y=a,
则曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,m=0,2,3,4,则m的值不可能是1,故④对.
故选:B.
点评:本题考查函数的奇偶性及运用,抽象函数的定义域和函数的图象,以及二次方程实根的分布,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
曲线y=cosx(-
≤x≤
)与x轴所围图形的面积为( )
| π |
| 2 |
| π |
| 2 |
| A、4 | B、2 | C、3 | D、1 |
按照如图的程序框图执行,则输出的A值为( )


| A、255 | B、257 |
| C、511 | D、513 |
函数f(x)=xex-a有两个零点,则实数a的取值范围是( )
A、-
| ||
B、a>-
| ||
| C、-e<a<0 | ||
| D、0<a<e |



