题目内容
6.设函数f(x)=2lnx+x2-2ax(a>0).(Ⅰ)若函数f(x)在区间[1,2]上的最小值为0,求实数a的值;
(Ⅱ)若x1,x2(x1<x2)是函数f(x)的两个极值点,且f(x1)-f(x2)>m恒成立,求实数m的取值范围.
分析 (Ⅰ)求导数,分类讨论,确定函数的单调性,利用函数f(x)在区间[1,2]上的最小值为0,求实数a的值;
(Ⅱ)f(x1)-f(x2)=(2lnx1+x12-2ax1)-(2lnx2+x22-2ax2)=$\frac{1}{{{x}_{1}}^{2}}$-x12+2lnx12,令x12=t,则t>1,g(t)=$\frac{1}{t}$-t-2lnt,x,求导,确定函数的单调性,求最值,即可求实数m的取值范围.
解答 解:(Ⅰ)f′(x)=$\frac{2({x}^{2}-ax+1)}{x}$,
0<a≤2,f′(x)≥0,f(x)在区间[1,2]上单调递增,∴f(x)min=f(1)=1-2a=0,∴a=$\frac{1}{2}$;
a>2,令f′(x)=0,则x1=$\frac{a-\sqrt{{a}^{2}-4}}{2}$,x2=$\frac{a+\sqrt{{a}^{2}-4}}{2}$,
2<a<$\frac{5}{2}$,x1=$\frac{a-\sqrt{{a}^{2}-4}}{2}$<1,x2=$\frac{a+\sqrt{{a}^{2}-4}}{2}$∈(1,2),
∴函数在(1,x1)内单调递减,在(x1,2)内单调递增,
∴f(x)min=f(x1)<f(1)=1-2a<0.
a≥$\frac{5}{2}$,x1=$\frac{a-\sqrt{{a}^{2}-4}}{2}$$≤\frac{1}{2}$,x2=$\frac{a+\sqrt{{a}^{2}-4}}{2}$≥2,
∴函数在(1,2)内单调递减,∴f(x)min=f(2)=2ln2+4-4a=0.
∴a=$\frac{1}{2}$ln2+1<$\frac{5}{2}$(舍去)
综上所述,a=$\frac{1}{2}$;
(Ⅱ)x1,x2是f′(x)=$\frac{2({x}^{2}-ax+1)}{x}$在(0,+∞)内的两个零点,是方程x2-ax+1=0的两个正根,
∴x1+x2=a>0,x1x2=1,△>0,∴a>2,∴x1>1
∴f(x1)-f(x2)=(2lnx1+x12-2ax1)-(2lnx2+x22-2ax2)=$\frac{1}{{{x}_{1}}^{2}}$-x12+2lnx12,
令x12=t,则t>1,g(t)=$\frac{1}{t}$-t-2lnt,
∴g′(t)=-$\frac{(t-1)^{2}}{t}$<0,
∴g(x)在(1,+∞)上单调递减,
∴g(t)>g(1)=0,
∴m≤0.
点评 本题考查导数知识的综合运用,考查函数的单调性与最值,正确构造函数,合理求导是关键.

| A. | [4,+∞) | B. | (0,$\frac{5}{2}$] | C. | [$\frac{5}{2}$,4] | D. | [$\frac{5}{2}$,+∞) |
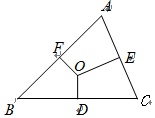 如图,在△ABC中,BC=a,AC=b,AB=c.O是△ABC的外心,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,则OD:OE:OF等于( )
如图,在△ABC中,BC=a,AC=b,AB=c.O是△ABC的外心,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,则OD:OE:OF等于( )| A. | a:b:c | B. | $\frac{1}{a}:\frac{1}{b}:\frac{1}{c}$ | C. | sinA:sinB:sinC | D. | cosA:cosB:cosC |
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |