题目内容
1.若复数z=$\frac{1+i}{1-i}$,$\overline{z}$为z的共轭复数,则($\overline{z}$)2017=-i.分析 利用复数代数形式的乘除运算化简,再由虚数单位i的性质求解.
解答 解:∵z=$\frac{1+i}{1-i}$=$\frac{(1+i)^{2}}{2}=i$,
∴$\overline{z}=-i$,
∴($\overline{z}$)2017=(-i)2017=-i.
故答案为:-i.
点评 本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.

练习册系列答案
相关题目
13.已知x,y是实数,i是虚数单位,$\frac{x}{1+i}=1-yi$,则复数x+yi在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.已知复数z1,z2在复平面内对应的点关于直线y=x对称,z1=1+2i,则$\frac{z_1}{z_2}$=( )
| A. | $\frac{3}{5}-\frac{4}{5}i$ | B. | $\frac{3}{5}+\frac{4}{5}i$ | C. | $\frac{4}{5}-\frac{3}{5}i$ | D. | $\frac{4}{5}+\frac{3}{5}i$ |
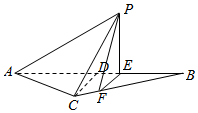 等腰△ABC的底边$AB=6\sqrt{6}$,高CD=3,点E是线段BD上异于点B,D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
等腰△ABC的底边$AB=6\sqrt{6}$,高CD=3,点E是线段BD上异于点B,D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.