题目内容
18.已知在数列{an}中,a1=1,an+1=2an+n-1,n∈N*.(1)证明:数列{an+n}是等比数列;
(2)求数列{an}的前n项和Sn.
分析 (1)由an+1=2an+n-1,n∈N*.变形为an+1+n+1=2(an+n),n∈N*.即可证明.
(2)由(1)得an+n=2n,利用等差数列与等比数列的求和公式即可得出.
解答 (1)证明:由an+1=2an+n-1,n∈N*.
可得an+1+n+1=2(an+n),n∈N*.
又a1+1=2,所以数列{an+n}是以2为首项,以2为公比的等比数列.
(2)解:由(1)得an+n=2n,
故an=2n-n,
所以数列{an}的前n项和Sn=$\frac{2({2}^{n}-1)}{2-1}$-$\frac{n(n+1)}{2}$=2n+1-2-$\frac{n(n+1)}{2}$.
点评 本题考查了数列递推关系、通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.将函数f(x)=$\sqrt{3}$sin2x-cos2x的图象向左平移φ(0<φ<$\frac{π}{2}$)个单位长度后得到函数y=g(x)的图象,若g(x)≤|g($\frac{π}{6}$)|对x∈R恒成立,则函数y=g(x)的单调递减区间是( )
| A. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) | B. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | ||
| C. | [kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$](k∈Z) | D. | [kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$](k∈Z) |
13.已知F1、F2是双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点M在E的渐近线上,且MF1与x轴垂直,sin∠MF2F1=$\frac{1}{3}$,则E的离心率为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
3.在数列{an}中,a1=2,2an+1=2an+1,则a2015的值是( )
| A. | 1009 | B. | 1008 | C. | 1010 | D. | 1011 |
10.已知$cosα=\frac{3}{5}$,$α∈(\frac{3π}{2},2π)$,则$cos(α-\frac{π}{4})$=( )
| A. | $\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{7\sqrt{2}}}{10}$ | C. | $\frac{{\sqrt{2}}}{10}$ | D. | $-\frac{{\sqrt{2}}}{10}$ |
7.已知正四面体棱长为4$\sqrt{2}$,则此正四面体外接球的表面积为( )
| A. | 36π | B. | 48π | C. | 64π | D. | 72π |
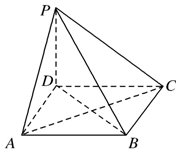 如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.
如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.