题目内容
已知函数
(1)求函数的最小正周期;
(2)当 时,求函数
时,求函数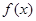 的值域;
的值域;
(3)先将函数 的图象向左平移
的图象向左平移 个单位得到函数
个单位得到函数 的图象,再将
的图象,再将 的图象横坐标扩大到原来的2倍纵坐标不变,得到函数
的图象横坐标扩大到原来的2倍纵坐标不变,得到函数 的图象,求证:直线
的图象,求证:直线 与
与 的图象相切于
的图象相切于
(1) ;(2)
;(2)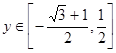 ;(3)详见解析
;(3)详见解析
解析试题分析:(1)本小题首先需要把函数化简可得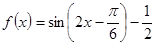 ,然后根据三角函数周期公式
,然后根据三角函数周期公式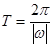 可求得目标函数最小正周期
可求得目标函数最小正周期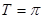 ;(2)首先根据
;(2)首先根据 的取值范围求得
的取值范围求得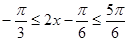 ,结合正弦函数的图像可求得
,结合正弦函数的图像可求得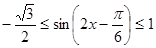 ,从而可求得函数的值域
,从而可求得函数的值域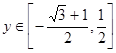 ;(3)首先根据函数图像的各种平移变化,可求得
;(3)首先根据函数图像的各种平移变化,可求得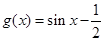 ,然后利用导数的几何意义求得曲线的切线方程
,然后利用导数的几何意义求得曲线的切线方程 ,从而可证明结论.
,从而可证明结论.
试题解析:(1)由已知可得: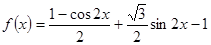
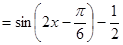
故函数的最小正周期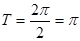
(2)因为 ,所以
,所以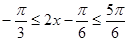
所以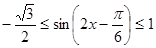
所以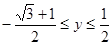
即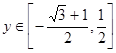
(3)将函数 的图象向左平移
的图象向左平移 个单位得到函数
个单位得到函数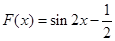 ,
,
再将 的图象横坐标扩大到原来的2倍纵坐标不变,
的图象横坐标扩大到原来的2倍纵坐标不变,
得到函数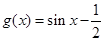 。
。
因为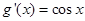 ,
,
所以切线的斜率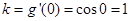 ,
,
而切点为
所以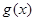 的切线方程为
的切线方程为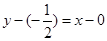 ,即
,即
所以直线 与
与 的图象相切于
的图象相切于
考点:1.三角函数的图像与性质;2.平移变换;3.导数的几何意义.

练习册系列答案
相关题目
 函数
函数 满足
满足 .
. 的单调递减区间;
的单调递减区间; 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且 ,求
,求 的取值范围.
的取值范围. ,
, .
. ,求
,求 的值;
的值;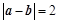 ,
, ,求
,求 的值.
的值. ,设∠CAB=α,
,设∠CAB=α, ,其中
,其中 ,求
,求 的值.
的值.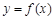 的图像关于点
的图像关于点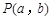 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数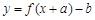 是奇函数”.
是奇函数”.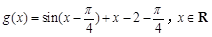 的图像向左平移
的图像向左平移 个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数
个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数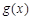 图像对称中心的坐标;
图像对称中心的坐标;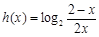 图像对称中心的坐标;
图像对称中心的坐标; 和
和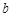 ,使得函数
,使得函数 ,且当
,且当 时,
时, 的最小值为2.
的最小值为2. 的值,并求
的值,并求 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ,再把所得图象向右平移
,再把所得图象向右平移 个单位,得到函数
个单位,得到函数 ,求方程
,求方程 在区间
在区间 上的所有根之和.
上的所有根之和.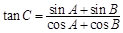 .
.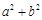 的取值范围.
的取值范围. 中,角
中,角 的对边分别为
的对边分别为 .
. ,求
,求 的值;
的值; ,求
,求 的值.
的值.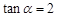 ,
, ,其中
,其中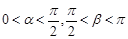 .
.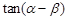 ;(2)求
;(2)求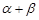 的值.
的值.