题目内容
设 函数
函数 满足
满足 .
.
(1)求 的单调递减区间;
的单调递减区间;
(2)设锐角 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且 ,求
,求 的取值范围.
的取值范围.
(1) ;(2)
;(2)
解析试题分析:(1)由 函数
函数 ,运用二倍角公式的逆运算,即可将
,运用二倍角公式的逆运算,即可将 化成一个角的和差的正余弦形式.再结合基本函数的单调性,通过解不等式即可得到
化成一个角的和差的正余弦形式.再结合基本函数的单调性,通过解不等式即可得到 的单调递减区间.
的单调递减区间.
(2)因为 ,结合余弦定理化简后再根据正弦定理,即可得到角B的值,又由(1)所得的函数关系,即可求出角A的范围.
,结合余弦定理化简后再根据正弦定理,即可得到角B的值,又由(1)所得的函数关系,即可求出角A的范围.
试题解析:(1)
由 得:
得: ,∴
,∴ ∴
∴
由 得:
得: ,
,
∴ 的单调递减区间为:
的单调递减区间为:
(2)∵ ,由余弦定理得:
,由余弦定理得: ,
,
即 ,由正弦定理得:
,由正弦定理得: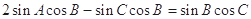 ,
, ,
, 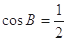 ,∴
,∴
∵△ 锐角三角形,∴
锐角三角形,∴ ,
,
∴ 的取值范围为
的取值范围为 .
.
考点:1.三角函数的二倍角公式.2.三角函数的化一公式.3.运用正弦定理、余弦定理解三角形.4.三角不等式的解法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +x)·cos(
+x)·cos( sin2x-
sin2x- .
.
 的最小正周期;
的最小正周期; ,求
,求 的值域.
的值域. .
. 的值;
的值; 的值.
的值. 
 ;
; ;
; ;
; ;
; .
.
 时,求函数
时,求函数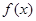 的值域;
的值域; 的图象向左平移
的图象向左平移 个单位得到函数
个单位得到函数 的图象,再将
的图象,再将 的图象,求证:直线
的图象,求证:直线 与
与
 ,sinα=
,sinα= ,tan(α-β)=-
,tan(α-β)=- ,求cosβ的值.
,求cosβ的值. sin2
sin2 +cos
+cos