题目内容
20.已知a=${∫}_{0}^{1}$(x一x2)dx,则二项式(x2-$\frac{12a}{x}$)6展开式中含x3的项的系数为-160.分析 先利用定积分求得a的值,再利用二项式定理的应用,二项式展开式的通项公式,求得含x3的项的系数.
解答 解:a=${∫}_{0}^{1}$(x一x2)dx=($\frac{{x}^{2}}{2}$-$\frac{{x}^{3}}{3}$)${|}_{0}^{1}$=$\frac{1}{6}$,
则二项式(x2-$\frac{12a}{x}$)6 =${{(x}^{2}-\frac{2}{x})}^{6}$ 的展开式的通项公式为Tr+1=${C}_{6}^{r}$•(-2)r•x12-3r,
令12-3r=3,求得r=3,可得含x3的项的系数为-8•${C}_{6}^{3}$=-160,
故答案为:-160.
点评 本题主要考查求定积分的值,二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
相关题目
15.如果实数xy满足$\left\{\begin{array}{l}{2x+y≤2}\\{x-y≥-1}\\{x+ay≤-1}\end{array}\right.$(a>0).目标函数z=ax+y有最大值,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,1) | B. | [1,2] | C. | (1,+∞) | D. | [$\frac{1}{2}$,+∞) |
7.某医院对治疗支气管肺炎的两种方案A,B进行比较研究,将志愿者分为两组,分别采用方案A和方案B进行治疗,统计结果如下:
(Ⅰ)完成上述列联表,并比较两种治疗方案有效的频率;
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
| 有效 | 无效 | 合计 | |
| 使用方案A组 | 96 | 120 | |
| 使用方案B组 | 72 | ||
| 合计 | 32 |
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
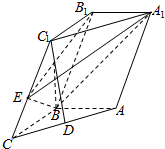 如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.
如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°. 如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.
如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.