题目内容
9.某公司为感谢全体员工的辛勤劳动,决定在年终答谢会上,通过摸球方式对全公司1000位员工进行现金抽奖.规定:每位员工从装有4个相同质地球的袋子中一次性随机摸出2个球,这4个球上分别标有数字a、b、c、d,摸出来的两个球上的数字之和为该员工所获的奖励额X(单位:元).公司拟定了以下三个数字方案:| 方案 | a | b | c | d |
| 一 | 100 | 100 | 100 | 500 |
| 二 | 100 | 100 | 500 | 500 |
| 三 | 200 | 200 | 400 | 400 |
(Ⅱ)分别计算方案二、方案三的平均数$\overline{X}$和方差s2,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
(Ⅲ)在投票选择方案二还是方案三时,公司按性别分层抽取100名员工进行统计,得到如下不完整的2×2列联表.请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
| 方案二 | 方案三 | 合计 | |
| 男性 | 12 | 48 | 60 |
| 女性 | 6 | 34 | 40 |
| 合计 | 18 | 82 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
分析 (Ⅰ)确定基本事件的个数,即可求X=200的概率;
(Ⅱ)求出相应的方差,即可得出结论;
(Ⅲ)计算K2,与临界值比较,即可得出结论.
解答 解:(Ⅰ)从a、b、c、d中取两个,共有ab、ac、ad、bc、bd、cd 这6个基本事件…(1分)
采取方案一,设X=200为事件A,它包含ab、ac、bc这3个基本事件
由于每个基本事件都是等可能的,所以$P(A)=\frac{3}{6}=\frac{1}{2}$…(3分)
(Ⅱ)依题意,求数据ab、ac、ad、bc、bd、cd的平均数$\overline{X}$和方差s2.${\overline{X}}_{2}=\frac{200+600+600+600+600+1000}{6}=600$,…(4分)${s}_{2}^{2}=\frac{1}{6}[{(200-600)}^{2}+{(600-600)}^{2}+{(600-600)}^{2}+{(600-600)}^{2}+{(600-600)}^{2}+{(1000-600)}^{2}]=\frac{160000}{3}$,…(5分)
${\overline{X}}_{3}=\frac{400+600+600+600+600+800}{6}=600$,…(6分)${s}_{3}^{2}=\frac{1}{6}[{(400-600)}^{2}+{(600-600)}^{2}+{(600-600)}^{2}+{(600-600)}^{2}+{(600-600)}^{2}+{(800-600)}^{2}]=\frac{40000}{3}$,…(7分)
${\overline{X}}_{2}={\overline{X}}_{3}$,${s}_{2}^{2}>{s}_{3}^{2}$,方案三的方差较小,相对均衡,选择方案三较好.…(8分)
(Ⅲ)
| 二 | 三 | 合计 | |
| 男性 | 12 | 48 | 60 |
| 女性 | 6 | 34 | 40 |
| 合计 | 18 | 82 | 100 |
直接计算得,${K}^{2}=\frac{100{(12×34-6×48)}^{2}}{60×40×18×82}≈0.407$,K2<2.706,…(11分)
所以不能以(1-P(K2≥2.706))×100%=90%的把握认为选择方案二或三与性别有关.…(12分)
点评 本题考查概率的计算,考查统计知识,考查独立性检验知识,考查学生分析解决问题的能力,属于中档题.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案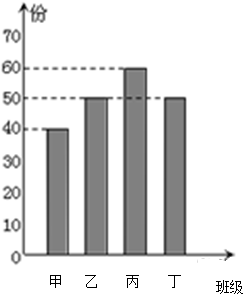 某研发公司研制出一款保护视力的护眼仪,并在新疆某中学的甲、乙、丙、丁四个班级中试用,这四个班级人数的条形图如下,为了了解学生护眼仪的使用情况,对四个班的学生进行了问卷调查,然后按分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
某研发公司研制出一款保护视力的护眼仪,并在新疆某中学的甲、乙、丙、丁四个班级中试用,这四个班级人数的条形图如下,为了了解学生护眼仪的使用情况,对四个班的学生进行了问卷调查,然后按分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:| 甲班 | 乙班 | 丙班 | 丁班 | |
| 满意 | 50% | 80% | 100% | 60% |
| 一般 | 25% | 0 | 0 | 0 |
| 不满意 | 25% | 20% | 0 | 40% |
(2)若需从调查问卷被选中且填写不满意的学生中再选2人进行访谈,求这两人中至少有一人是丁班学生的概率.
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
| A. | 2 | B. | 4 | C. | 8 | D. | 12 |
 为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):
为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):147 161 170 180 163 172 178 167 191 182
181 173 174 165 158 154 159 189 168 169
(Ⅰ)完成如下频数分布表,并作频率分布直方图;
| 通行数量区间 | [145,155) | [155,165) | [165,175) | [175,185) | [185,195) |
| 频数 |
| A. | a>3 | B. | a≥3 | C. | a≥-1 | D. | a>-1 |