题目内容
17.“cos2α=0”是“sinα=cosα”的( )| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
分析 由sinα=cosα,可得cos2α=cos2α-sin2α=0;反之cos2α=cos2α-sin2α=0,可得cosα=±sinα.即可判断出结论.
解答 解:由sinα=cosα⇒cos2α=cos2α-sin2α=0;
由cos2α=cos2α-sin2α=0,⇒cosα=±sinα.
∴“cos2α=0”是“sinα=cosα”的必要不充分条件.
故选:C.
点评 本题考查了倍角公式、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.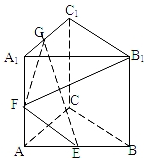 正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
 正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )| A. | $\frac{5}{6}$ | B. | $\frac{3}{5}$ | C. | $\frac{3\sqrt{3}}{10}$ | D. | $\frac{3\sqrt{6}}{10}$ |
8.在平面直角坐标系中,方程$\frac{|x|}{2}$+$\frac{|y|}{4}$=1所表示的曲线是( )
| A. | 椭圆 | B. | 三角形 | C. | 菱形 | D. | 两条平行线 |
12.设点P为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{4}=1({a>2})$上一点,F1,F2分别为C的左、右焦点,且∠F1PF2=60°,则△PF1F2的面积为( )
| A. | $4\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
2.将函数f(x)=sinωx(ω是正整数)的图象向右平移$\frac{π}{6}$个单位,所得曲线在区间$(\frac{4π}{3},\frac{3π}{2})$内单调递增,则ω的最大值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
9.某公司为感谢全体员工的辛勤劳动,决定在年终答谢会上,通过摸球方式对全公司1000位员工进行现金抽奖.规定:每位员工从装有4个相同质地球的袋子中一次性随机摸出2个球,这4个球上分别标有数字a、b、c、d,摸出来的两个球上的数字之和为该员工所获的奖励额X(单位:元).公司拟定了以下三个数字方案:
(Ⅰ)如果采取方案一,求X=200的概率;
(Ⅱ)分别计算方案二、方案三的平均数$\overline{X}$和方差s2,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
(Ⅲ)在投票选择方案二还是方案三时,公司按性别分层抽取100名员工进行统计,得到如下不完整的2×2列联表.请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 方案 | a | b | c | d |
| 一 | 100 | 100 | 100 | 500 |
| 二 | 100 | 100 | 500 | 500 |
| 三 | 200 | 200 | 400 | 400 |
(Ⅱ)分别计算方案二、方案三的平均数$\overline{X}$和方差s2,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
(Ⅲ)在投票选择方案二还是方案三时,公司按性别分层抽取100名员工进行统计,得到如下不完整的2×2列联表.请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
| 方案二 | 方案三 | 合计 | |
| 男性 | 12 | 48 | 60 |
| 女性 | 6 | 34 | 40 |
| 合计 | 18 | 82 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
5.若集合A={y|y=lgx},B={x|y=$\sqrt{x}$},则集合A∩B=( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | ∅ |
4. 《九章算术•商功》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的侧面积为( )
《九章算术•商功》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的侧面积为( )
 《九章算术•商功》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的侧面积为( )
《九章算术•商功》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的侧面积为( )| A. | 4 | B. | 6+4$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 2 |