题目内容
已知等差数列{an}的首项a1=3,公差d≠0,其前n项和为Sn,且a1,a4,a13分别是等比数列{bn}的第2项,第3项,第4项.
(1)求数列{an}与{bn}的通项公式;
(2)证明: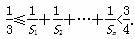
解:(1)设等比数列{bn}的公比为q.
∵a1,a4,a13分别是等比数列{bn}的b2,b3,b4.且a1=3
∴(a1+3d)2=a1(a1+12d)
即(3+3d)2=3·(3+12d),∴9d2+18d+9=9+36d
整理得:d=2或d=0(舍),∴an=3+2(n-1)=2n+1
q= =
= =
= =3,b1=
=3,b1= =
= =
= =1,∴bn=3n-1
=1,∴bn=3n-1
(2)证明:由(1)知:
Sn=n·a1+ ·d=3n+n2-n=n2+2n
·d=3n+n2-n=n2+2n


练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
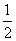 ,an,Sn成等差数列.
,an,Sn成等差数列.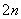 =
=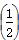 bn,设Cn=
bn,设Cn=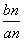 ,求数列{Cn}的前n项和Tn.
,求数列{Cn}的前n项和Tn. =2n-7(n∈N*,n>1),则当an取得最小值时n的值是( )
=2n-7(n∈N*,n>1),则当an取得最小值时n的值是( ) 的倾斜角的变化范围是( )
的倾斜角的变化范围是( )
 ,这样的点P的个数是( )
,这样的点P的个数是( )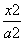 +
+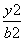 =1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,在x轴负半轴上有一点B,满足
=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,在x轴负半轴上有一点B,满足 ,AB⊥AF2.
,AB⊥AF2.
 y-3=0的最大距离等于椭圆长轴的长,求椭圆C的方程.
y-3=0的最大距离等于椭圆长轴的长,求椭圆C的方程.