题目内容
若直线ax+y+2=0与A(-2,3),B(3,2)的线段有交点,则a的取值范围为( )
A、(-∞,-
| ||||
B、(-∞,-
| ||||
C、[
| ||||
D、[-
|
考点:直线的斜率
专题:直线与圆
分析:直线ax+y+2=0过定点P(0,-2),利用斜率计算公式可得kPA,kPB.由于直线ax+y+2=0与A(-2,3),B(3,2)的线段有交点,可得-a≥kPB或-a≤kPA,解出即可.
解答:
解:直线ax+y+2=0过定点P(0,-2),
kPA=
=-
,kPB=
=
.
∵直线ax+y+2=0与A(-2,3),B(3,2)的线段有交点,
∴-a≥kPB或-a≤kPA,
解得a≤-
或a≥
.
∴a的取值范围为(-∞,-
]∪[
,+∞).
故选:A.
kPA=
| 3-(-2) |
| -2 |
| 5 |
| 2 |
| 2-(-2) |
| 3-0 |
| 4 |
| 3 |
∵直线ax+y+2=0与A(-2,3),B(3,2)的线段有交点,
∴-a≥kPB或-a≤kPA,
解得a≤-
| 4 |
| 3 |
| 5 |
| 2 |
∴a的取值范围为(-∞,-
| 4 |
| 3 |
| 5 |
| 2 |
故选:A.
点评:本题考查了直线的斜率计算公式及其意义,考查了计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合A={0,2,3},B={x|x2-2x=0},则A∩B=( )
| A、{2} | B、{0,2} |
| C、{0,3} | D、{2,3} |

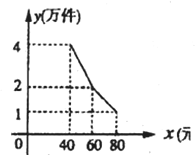 为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.
为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.