题目内容
如图所示，在四面体A-BCD中，若截面PQMN是正方形，则在下列命题中错误的为（ ）
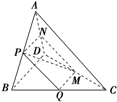
| A、AC⊥BD |
| B、AC∥截面PQMN |
| C、AC=BD |
| D、BD∥截面PQMN |
考点：直线与平面平行的性质,直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：首先由正方形中的线线平行推导线面平行，再利用线面平行推导线线平行，这样就把AC、BD平移到正方形内，即可利用平面图形知识做出判断．
解答：
解：因为截面PQMN是正方形，所以PQ∥MN、QM∥PN，
则PQ∥平面ACD、QM∥平面BDA，
所以PQ∥AC，QM∥BD，
由PQ⊥QM可得AC⊥BD，故A正确；
由PQ∥AC可得AC∥截面PQMN，故B正确；
同理D正确；
综上C是错误的．
故选C．
则PQ∥平面ACD、QM∥平面BDA，
所以PQ∥AC，QM∥BD，
由PQ⊥QM可得AC⊥BD，故A正确；
由PQ∥AC可得AC∥截面PQMN，故B正确；
同理D正确；
综上C是错误的．
故选C．
点评：本题主要考查线面平行的性质与判定．
练习册系列答案
相关题目
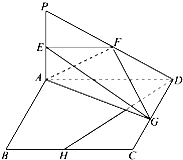如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且AD=2PA，E，F，G，H分别是线段PA，PD，CD，BC的中点．
如图，锐角三角形ABC内接于⊙O，∠ABC=60°，∠BAC=40°，作OE⊥AB交劣弧