题目内容
9．若复数（x2-1）+（x+1）i为纯虚数，则实数x的值为（ ）| A． | 1 | B． | -1 | C． | 1或-1 | D． | 不存在 |
分析 利用纯虚数的定义即可得出．
解答 解：∵复数（x2-1）+（x+1）i为纯虚数，
∴x2-1=0，x+1≠0，
解得x=1．
故选：A．
点评 本题考查了纯虚数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
19．下列说法错误的是（ ）
| A． | 在统计学中，独立性检验是检验两个分类变量是否有关系的一种统计方法 | |
| B． | 在残差图中，残差分布的带状区域的宽度越狭窄，其模拟的效果越好 | |
| C． | 线性回归方程对应的直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$至少经过其样本数据点中的一个点 | |
| D． | 在回归分析中，相关指数R2越大，模拟的效果越好 |
20．若集合P={-2，0，2}，i是虚数单位，则（ ）
| A． | 2i∈P | B． | $\frac{2}{i}$∈P | C． | （$\sqrt{2}$i）2∈P | D． | $\frac{2}{{i}^{3}}$∈P |
17．下列不等式中，正确的是（ ）
| A． | tan$\frac{4π}{7}$＞tan$\frac{3π}{7}$ | B． | tan$\frac{2π}{5}$＜tan$\frac{3π}{5}$ | ||
| C． | tan（-$\frac{13π}{7}$）＞tan（-$\frac{15π}{8}$） | D． | tan（-$\frac{13π}{4}$）＜tan（-$\frac{12π}{5}$） |
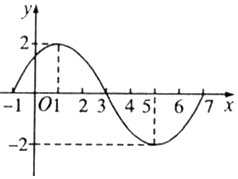已知函数y=Asin（ωx+φ）（A＞0，ω＞0）在一个周期内的图象如图所示．