题目内容
7.已知过球面上A,B,C三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2,则球面的面积是$\frac{64π}{9}$.分析 由AB=BC=CA=2,求得△ABC的外接圆半径为r,再由R2-($\frac{1}{2}$R)2=$\frac{4}{3}$,求得球的半径,再用面积求解.
解答 解:因为AB=BC=CA=2,
所以△ABC的外接圆半径为r=$\frac{2\sqrt{3}}{3}$.
设球半径为R,则R2-($\frac{1}{2}$R)2=$\frac{4}{3}$,
所以R2=$\frac{16}{9}$,
所以S=4πR2=$\frac{64π}{9}$.
故答案为$\frac{64π}{9}$.
点评 本题主要考查球的球面面积,涉及到截面圆圆心与球心的连线垂直于截面,这是求得相关量的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15.已知四面体A-BCD中,△ABC和△BCD都是边长为6的正三角形,则当四面体的体积最大时,其外接球的表面积是( )
| A. | 60π | B. | 30π | C. | 20π | D. | 15π |
17.已知某几何体的三视图如图所示,则该几何体的体积为( )
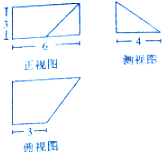

| A. | 36 | B. | 30 | C. | 24 | D. | 20 |