题目内容
8．A、B分别是复数z1、z2在复平面内对应的点，O是原点，若|z1+z2|=|z1-z2|，则三角形AOB一定是（ ）| A． | 等腰三角形 | B． | 直角三角形 | C． | 等边三角形 | D． | 等腰直角三角形 |
分析 利用复数的几何意义，结合向量的性质进行判断即可．
解答 解：设复数z1、z2在复平面内对应的向量为$\overrightarrow{{z}_{1}}$，$\overrightarrow{{z}_{2}}$，
则由|z1+z2|=|z1-z2|，得|$\overrightarrow{{z}_{1}}$+$\overrightarrow{{z}_{2}}$，|=|$\overrightarrow{{z}_{1}}$-$\overrightarrow{{z}_{2}}$|，
则向量$\overrightarrow{{z}_{1}}$，$\overrightarrow{{z}_{2}}$为邻边的平行四边形为矩形，
则角形AOB一定是直角三角形，
故选：B．
点评 本题主要考查复数几何意义的意义，根据条件转化为向量是解决本题的关键．
练习册系列答案
相关题目
18．集合A={x|3x+2＞0}，B={x|$\frac{x+1}{x-3}$＜0}，则A∩B=（ ）
| A． | （-1，+∞） | B． | （-1，-$\frac{2}{3}$） | C． | （3，+∞） | D． | （-$\frac{2}{3}$，3） |
19．已知等差数列{an}中，a1+a4+a7=$\frac{5}{4}π$，那么cos（a3+a5）=（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | -$\frac{\sqrt{2}}{2}$ |
16．两列火车从同一站台沿相反方向开去，走了相同的路程，设两列火车的位移向量分别为$\overrightarrow{a}$和$\overrightarrow{b}$，则下列说法中错误的是（ ）
| A． | $\overrightarrow{a}$与$\overrightarrow{b}$为平行向量 | B． | $\overrightarrow{a}$与$\overrightarrow{b}$为模相等的向量 | ||
| C． | $\overrightarrow{a}$与$\overrightarrow{b}$为共线向量 | D． | $\overrightarrow{a}$与$\overrightarrow{b}$为相等的向量 |
3．
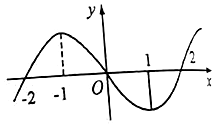已知f（x）在R上是可导函数，f（x）的图象如图所示，则不等式f′（x）＞0的解集为（ ）
已知f（x）在R上是可导函数，f（x）的图象如图所示，则不等式f′（x）＞0的解集为（ ）| A． | （-2，0）∪（2，+∞） | B． | （-∞，2）∪（2，+∞） | C． | （-∞，-1）∪（1，+∞） | D． | （-2，-1）∪（1，2） |
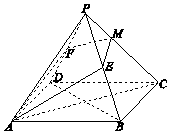如图，在正四棱锥P-ABCD中，PA=AB，E，F分别为PB，PD的中点．