题目内容
在含有3件次品的10件产品中,取出n(n≤10,n∈N*)件产品,
记ξn表示取出的次品数,算得如下一组期望值Eξn:
当n=1时,Eξ1=0×
+1×
=
;
当n=2时,Eξ2=0×
+1×
+2×
=
;
当n=3时,Eξ3=0×
+1×
+2×
+3×
=
;
…
观察以上结果,可以推测:若在含有M件次品的N件产品中,取出n(n≤N,n∈N*)件产品,记ξn表示取出的次品数,则Eξn= .
记ξn表示取出的次品数,算得如下一组期望值Eξn:
当n=1时,Eξ1=0×
| ||||
|
| ||||
|
| 3 |
| 10 |
当n=2时,Eξ2=0×
| ||||
|
| ||||
|
| ||||
|
| 6 |
| 10 |
当n=3时,Eξ3=0×
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| 9 |
| 10 |
…
观察以上结果,可以推测:若在含有M件次品的N件产品中,取出n(n≤N,n∈N*)件产品,记ξn表示取出的次品数,则Eξn=
考点:归纳推理
专题:操作型,推理和证明
分析:分析已知中的数塔,可知,M=3,N=10时,Eξn=
,即可得出结论.
| Mn |
| N |
解答:
解:由题意,M=3,N=10时,Eξn=
,
由此可得,若在含有M件次品的N件产品中,取出n(n≤N,n∈N*)件产品,记ξn表示取出的次品数,则Eξn=
故答案为:
.
| Mn |
| N |
由此可得,若在含有M件次品的N件产品中,取出n(n≤N,n∈N*)件产品,记ξn表示取出的次品数,则Eξn=
| Mn |
| N |
故答案为:
| Mn |
| N |
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
极坐标系中的点(2,0)到直线θ=
的距离是( )
| π |
| 4 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
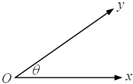 如图,在平面斜坐标系xOy中,∠xOy=θ,平面上任意一点P关于斜坐标系的斜坐标这样定义:若
如图,在平面斜坐标系xOy中,∠xOy=θ,平面上任意一点P关于斜坐标系的斜坐标这样定义:若