题目内容
给出两个命题:命题p:方程4x2+4(m-2)x+1=0无实数根;命题q:函数y=(3-m)x为增函数.若“p或q”为真命题,求实数m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:对两个条件化简,求出各自成立时参数所满足的范围,由“p或q”为真命题知p,q中至少有一个为真命题,求出m的范围.
解答:
解:若p为真命题,则△=16(m-2)2-16<0
∴1<m<3.
若q为真命题,则3-m>1,∴m<2.…(6分)
又“p或q”为真命题
∴p,q中至少有一个为真命题.

∴由图得:实数m的取值范围是(-∞,3). …(12分)
∴1<m<3.
若q为真命题,则3-m>1,∴m<2.…(6分)
又“p或q”为真命题
∴p,q中至少有一个为真命题.

∴由图得:实数m的取值范围是(-∞,3). …(12分)
点评:本题考查命题的真假判断与运用,解答本题的关键是由“p或q”为真命题知p,q中至少有一个为真命题,熟练掌握复合命题真假的判断方法很重要.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
从分别写有A,B,C,D,E的五张卡片中任取两张,这两张的字母顺序恰好相邻的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
从装有2个红球和2个黒球的口袋内任取2个球,则互斥而不对立的两个事件是( )
| A、“至少有一个黑球”与“都是红球” |
| B、“至少有一个黒球”与“都是黒球” |
| C、“恰有m个黒球”与“恰有2个黒球” |
| D、“至少有一个黒球”与“至少有1个红球” |
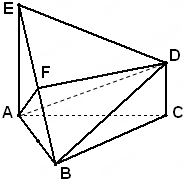 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证: