题目内容
11.已知$\overrightarrow{a}$=(1,2,-y),$\overrightarrow{b}$=(x,1,2),且($\overrightarrow{a}$+2$\overrightarrow{b}$)∥(2$\overrightarrow{a}$-$\overrightarrow{b}$),则x+y=$\frac{7}{2}$.分析 利用向量坐标运算性质、向量共线定理即可得出.
解答 解:$\overrightarrow{a}$+2$\overrightarrow{b}$=(1+2x,4,-y+4)
2$\overrightarrow{a}$-$\overrightarrow{b}$=(2-x,3,-2y-2),
∵($\overrightarrow{a}$+2$\overrightarrow{b}$)∥(2$\overrightarrow{a}$-$\overrightarrow{b}$),
∴存在实数k使得$\overrightarrow{a}$+2$\overrightarrow{b}$=k(2$\overrightarrow{a}$-$\overrightarrow{b}$),
∴$\left\{\begin{array}{l}{1+2x=k(2-x)}\\{4=3k}\\{-y+4=k(-2y-2)}\end{array}\right.$,
解得x=$\frac{1}{2}$,y=-4.
∴x+y=-$\frac{7}{2}$,
故答案为:-$\frac{7}{2}$.
点评 本题考查了向量坐标运算性质、向量共线定理,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.下列说法正确的是( )
| A. | 直线的倾斜角的取值范围是[0°,180°] | |
| B. | 若直线的倾斜角为90°,则这条直线与y轴平行 | |
| C. | 任意一条直线都有倾斜角和斜率 | |
| D. | 若直线l的倾斜角为锐角,则它的斜率大于0;若直线l的倾斜角为钝角,则它的斜率小于0 |
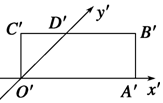 如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )
如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )