题目内容
20.已知甲袋中装有大小、形状、质地、相同的3个白球和2个红球,乙袋中装有1个白球和4个红球,现从甲、乙两袋中各摸一个球,试求:(1)两球都是红球的概率;
(2)恰有一个是红球的概率;
(3)至少有一个是红球的概率.
分析 (1)先求出基本事件总数,再求出两球都是红球包含的基本事件,由此能求出两球都是红球的概率.
(2)先求出基本事件总数,再求出恰有一个是红球包含的基本事件,由此能求出恰有一个是红球的概率.
(3)至少有一个是红球的对立事件是两个球都是白球,由此利用对立事件概率计算公式能求出至少有一个是红球的概率.
解答 解:(1)甲袋中装有大小、形状、质地、相同的3个白球和2个红球,
乙袋中装有1个白球和4个红球,现从甲、乙两袋中各摸一个球,
基本事件总数n=${C}_{5}^{1}{C}_{5}^{1}$=25,
两球都是红球包含的基本事件m1=${C}_{2}^{1}{C}_{4}^{1}$=8,
∴两球都是红球的概率p1=$\frac{{m}_{1}}{n}$=$\frac{8}{25}$.
(2)基本事件总数n=${C}_{5}^{1}{C}_{5}^{1}$=25,
恰有一个是红球包含的基本事件m2=${C}_{2}^{1}{C}_{1}^{1}+{C}_{3}^{1}{C}_{4}^{1}$=14,
∴恰有一个是红球的概率p1=$\frac{{m}_{2}}{p}$=$\frac{14}{25}$.
(3)基本事件总数n=${C}_{5}^{1}{C}_{5}^{1}$=25,
至少有一个是红球的对立事件是两个球都是白球,
∴至少有一个是红球的概率p3=1-$\frac{{C}_{3}^{1}{C}_{1}^{1}}{{C}_{5}^{1}{C}_{5}^{1}}$=$\frac{3}{25}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式和对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
20.“a=2”是“直线ax+2y-1=0与x+(a-1)y+1=0互相平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
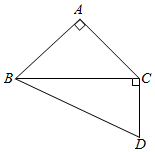 如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.
如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.