Question

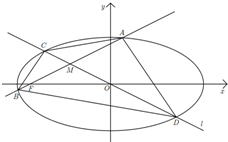如图，已知椭圆E：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

3

2

，过左焦点F（-

3

，0）且斜率为k的直线交椭圆E于A，B两点，线段AB的中点为M，直线l：x+4ky=0交椭圆E于C，D两点．
（Ⅰ）求椭圆E的方程；
（Ⅱ）求证：点M在直线l上；
（Ⅲ）是否存在实数k，使得三角形BDM的面积是三角形ACM的3倍？若存在，求出k的值；若不存在，说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）由椭圆的离心率、焦点坐标及b²=a²-c²联立求得a，b的值，则椭圆方程可求；
（Ⅱ）设出直线AB的方程，和（Ⅰ）中求出的椭圆方程联立后化为关于x的一元二次方程，利用根与系数关系和中点坐标公式求得M坐标，代入直线l：x+4ky=0验证即可；
（Ⅲ）由（Ⅱ）知点A到直线CD的距离与点B到直线CD的距离相等，由△BDM的面积是△ACM面积的3倍推得M为OC中点，联立直线l的方程和椭圆方程后结合根与系数关系求得M坐标，由M的坐标相等列式求得k的值．

解答： （Ⅰ）解：由题意可知e=

c

a

=

3

2

，c=

3

，于是a=2，
∴b2=a2-c2=22-(

3

)2=1，
∴椭圆的标准方程为

x2

4

+y2=1；
（Ⅱ）证明：设A（x₁，y₁），B（x₂，y₂），M（x₀，y₀），
联立

y=k(x+ 3 ) x2 4 +y2=1

，得(4k2+1)x2+8

3

k2x+12k2-4=0．
x1+x2=

-8 3 k2

4k2+1

，x0=

x1+x2

2

=

-4 3 k2

4k2+1

，y0=k(x0+

3

)=

3 k

4k2+1

，
∴M（

-4 3 k2

4k2+1

，

3 k

4k2+1

）．
∵

-4 3 k2

4k2+1

+4k•

3 k

4k2+1

=0，
∴M在直线l上；
（Ⅲ）解：由（Ⅱ）知点A到直线CD的距离与点B到直线CD的距离相等，
若△BDM的面积是△ACM面积的3倍，
则|DM|=3|CM|，
∵|OD|=|OC|，于是M为OC中点，
设点C的坐标为（x₃，y₃），则y0=

y3

2

．
联立

x=-4ky x2 4 +y2=1

，解得y3=±

1

4k2+1

．
于是

1

2 4k2+1

=

3 |k|

4k2+1

，解得k2=

1

8

，
∴k=±

2

4

．

点评：本题主要椭圆方程的求法，考查了直线与椭圆的位置关系的应用，直线与曲线联立，根据方程的根与系数的关系求解，是处理这类问题的最为常用的方法，但圆锥曲线的特点是计算量比较大，要求考试具备较强的运算推理的能力，是难题．