题目内容
6.已知f(x)=3x-a×3-x是偶函数.则:(1)a=-1;
(2)$f(x)<\frac{10}{3}$的解集为(-1,1).
分析 (1)根据f(-x)=f(x),求得a的值.
(2)不等式即(3x-3)•(3x-$\frac{1}{3}$)<0,即 $\frac{1}{3}$<3x<3,由此求得x的范围.
解答 解:(1)∵f(x)=3x-a×3-x是偶函数,则f(-x)=f(x),即 3-x-a•3x=3x-a•3-x,
即(3-x-3x)=-a(3-x-3x),∴-a=1,即a=-1,f(x)=3x +3-x,
故答案为:-1.
(2)$f(x)<\frac{10}{3}$,即 3x +3-x <$\frac{10}{3}$,即 32x-$\frac{10}{3}$•3x+1<0,即(3x-3)•(3x-$\frac{1}{3}$)<0,
∴$\frac{1}{3}$<3x<3,∴-1<x<1.
故答案为:(-1,1)
点评 本题主要考查偶函数的定义和性质,解指数不等式,属于中档题.

练习册系列答案
相关题目
16.如果集合U={1,2,3,4,5,6,7,8},A={2,3,5,8},B={1,3,5,7},那么(∁UA)∩B等于( )
| A. | {3,5} | B. | {1,3,4,5,6,7,8} | C. | {2,8} | D. | {1,7} |
1.下列四个命题中正确的是( )
| A. | 若a>b,c>d,则ac>bd | B. | 若ab≥0,则|a+b|=|a|+|b| | ||
| C. | 若x>2,则函数y=x+$\frac{1}{x}$有最小值2 | D. | 若a<b<0,则a2<ab<b2 |
11.F是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点,P为C上一动点,点A坐标为(1,1),则|PA|+|PF|的最小值为( )
| A. | 4+$\sqrt{5}$ | B. | 4-$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
18.实数a=0.33,b=log30.3,c=30.3的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
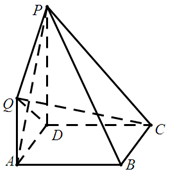 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,$QA=AB=\frac{1}{2}PD$.
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,$QA=AB=\frac{1}{2}PD$.