题目内容
5.求证:sin3θ(1+cotθ)+cos3θ(1+tanθ)=sinθ+cosθ.并证明.分析 根据三角函数的恒等式证明即可.
解答 证明:sin3θ(1+cotθ)+cos3θ(1+tanθ)
=sin3θ(1+$\frac{cosθ}{sinθ}$)+cos3θ(1+$\frac{sinθ}{cosθ}$)
=sin3θ+sin2θcosθ+cos3θ+cos2θsinθ
=(sinθ+cosθ)(sin2θ-sinθcosθ+cos2θ)+sin2θcosθ+cos2θsinθ
=(sinθ+cosθ)(1-sinθcosθ)+sin2θcosθ+cos2θsinθ
=sinθ+cosθ-sin2θcosθ-cos2θsinθ+sin2θcosθ+cos2θsinθ
=sinθ+cosθ.
点评 本题考查了三角函数的恒等变换,是一道基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
13.已知函数f(x)=$\sqrt{x+1}$+log2017(2-x)的定义域为( )
| A. | (-2,1] | B. | [1,2] | C. | [-1,2) | D. | (-1,2) |
10.已知任意两个向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,若$\overrightarrow{OA}$=$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{OB}$=$\overrightarrow{a}$+2$\overrightarrow{b}$,$\overrightarrow{OC}$=2$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{OD}$=$\overrightarrow{a}$-$\overrightarrow{b}$,则下列结论正确的是( )
| A. | A,B,C三点共线 | B. | A,B,D三点共线 | C. | A,C,D三点共线 | D. | B,C,D三点共线 |
15.若a0+a1(2x-1)+a2(2x-1)2+a3(2x-1)3+a4(2x-1)4+a5(2x-1)5=x5,则a2=( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{16}$ | D. | $\frac{5}{32}$ |
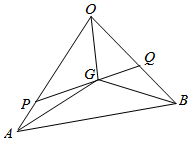 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.