题目内容
13.已知函数f(x)=$\sqrt{x+1}$+log2017(2-x)的定义域为( )| A. | (-2,1] | B. | [1,2] | C. | [-1,2) | D. | (-1,2) |
分析 根据函数的解析式,列出使函数解析式有意义的不等式组,求出解集即可.
解答 解:函数f(x)=$\sqrt{x+1}$+log2017(2-x),
要使函数有意义:需满足$\left\{\begin{array}{l}{x+1≥0}\\{2-x>0}\end{array}\right.$,
解得:-1≤x<2.
故选C.
点评 本题考查了求函数定义域的应用问题,解题的关键是列出使函数解析式有意义的不等式组,是基础题目.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18.设F1、F2为椭圆的两个焦点,M为椭圆上一点,MF1⊥MF2,且|MF2|=|MO|(其中点O为椭圆的中心),则该椭圆的离心率为( )
| A. | $\sqrt{3}$-1 | B. | 2-$\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.对一个容器为N的总体抽取容量为n的样本,当选择简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为a、b、c,则( )
| A. | a=b<c | B. | b=c<a | C. | a=c<b | D. | a=b=c |
6.甲、乙两位同学本学期几次数学考试的平均成绩很接近,为了判断甲、乙两名同学成绩哪个稳定,需要知道这两个人的( )
| A. | 中位数 | B. | 众数 | C. | 方差 | D. | 频率分布 |
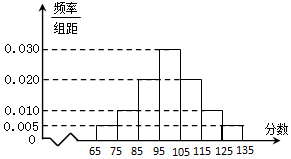 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图: 某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).
某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).