题目内容
5.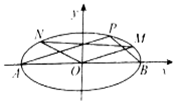 如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.
如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.(1)求椭圆C的方程;
(2)判断△OMN的面积是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
分析 (1)由题意可知a=2,直线的斜率公式,k1k2=-$\frac{1}{4}$,及y22=$\frac{{b}^{2}({2}^{2}-{x}^{2})}{{2}^{2}}$,即可求得b的值,即可求得椭圆C的方程;
(2)设直线l的方程,代入椭圆方程,由韦达定理,及直线的斜率公式,即可求得2t2-4k2=1,利用弦长公式及三角形的面积公式,即可求得△OMN的面积为定值1.
解答 解:(1)由题意可知:a=2,设P(x,y),(x≠±2,y≠±b),则y22=$\frac{{b}^{2}({2}^{2}-{x}^{2})}{{2}^{2}}$,
则直线AP斜率k1=$\frac{y}{x+2}$,直线BP的斜率k2=$\frac{y}{x-2}$,
则k1k2=$\frac{y}{x+2}$•$\frac{y}{x-2}$=$\frac{{y}^{2}}{{x}^{2}-4}$=-$\frac{{b}^{2}}{4}$=-$\frac{1}{4}$,
∴b=1,
椭圆的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)设直线MN的方程为y=kx+t,M(x1,y1),N(x2,y2),
则$\left\{\begin{array}{l}{y=kx+t}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,整理得:(4k2+1)x2+8ktx+4t2-4=0,
由韦达定理可知:x1+x2=-$\frac{8kt}{4{k}^{2}+1}$,x1x2=$\frac{4{t}^{2}-4}{4{k}^{2}+1}$,
由k1k2=-$\frac{1}{4}$,则$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{2}}{{x}_{2}}$=-$\frac{1}{4}$,
则4y1y2+x1x2=0,4(kx1+t)(kx2+t)+x1x2=0,
整理得:(4k2+1)x1x2+4kt(x1+x2)+4t2=0,
:(4k2+1)×$\frac{4{t}^{2}-4}{4{k}^{2}+1}$+4kt(-$\frac{8kt}{4{k}^{2}+1}$)+4t2=0,整理得:2t2-4k2=1,
丨MN丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,
=$\sqrt{1+{k}^{2}}$•$\sqrt{(-\frac{8kt}{4{k}^{2}+1})^{2}-4×\frac{4{t}^{2}-4}{4{k}^{2}+1}}$=2$\sqrt{2}$$\sqrt{\frac{{k}^{2}+1}{4{k}^{2}+1}}$,
由O到MN的距离d=$\frac{丨t丨}{\sqrt{1+{k}^{2}}}$,
△OMN的面积S,S=$\frac{1}{2}$×2$\sqrt{2}$$\sqrt{\frac{{k}^{2}+1}{4{k}^{2}+1}}$×$\frac{丨t丨}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$×$\frac{丨t丨}{\sqrt{2{t}^{2}}}$=1.
∴△OMN的面积1.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,韦达定理,弦长公式,点到直线的距离公式,考查计算能力,属于中档题.

| A. | 0<a≤5 | B. | a<5 | C. | 0<a<5 | D. | a≥5 |
| A. | {a|a<$\frac{1}{3}$} | B. | {a|0<a≤$\frac{1}{3}$} | C. | {a|a≤$\frac{1}{3}$} | D. | {a|a≥$\frac{1}{3}$} |
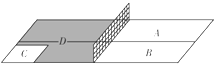 乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求:
乓球台面被网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A、B,乙被划分为两个不相交的区域C、D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为$\frac{1}{2}$,在D上的概率为$\frac{1}{3}$;对落点在B上的来球,小明回球的落点在C上的概率为$\frac{1}{5}$,在D上的概率为$\frac{3}{5}$.假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响.求: