题目内容

13．已知幂函数y=xm2-2m-3（m∈Z）的图象与x、y轴都无公共交点，且图象关于原点中心对称，求m的值，并且画出它的图象．

分析 由题意知，m2-2m-3＜0，且 m2-2m-3为奇数，解此不等式组可得m的值．

解答 解：幂函数y=xm2-2m-3（m∈Z）的图象与x、y轴都无公共交点，且图象关于原点中心对称，
∴m2-2m-3＜0，且 m2-2m-3为奇数，即-1＜m＜3 且 m2-2m-3 为奇数，
∴m=0或2，
∴y=x-3，
其图象为：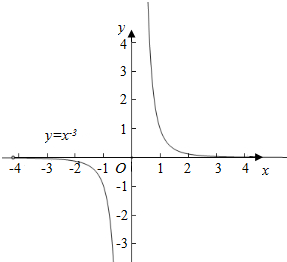

点评 本题考查幂函数的定义及幂函数的性质，关键是确定幂指数 m2-2m-3 所满足的条件．

练习册系列答案
相关题目
3．“an=2n，n∈N*”是“数列{an}是等差数列”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
4．已知：α、β为△ABC的内角且cosα=$\frac{1}{3}$，cos（α+β）=-$\frac{2}{3}$，求sinβ的值．
1．若log${\;}_{\sqrt{3}}$2=a，则log123=$\frac{1}{1+a}$．
8．已知定义域为R的奇函数f（x）满足：当x∈（0，+∞）时，f（x）=x（x+2）．
（1）求f（x）的解析式，并讨论f（x）的单调性；
（2）若实数x满足f（x2-bx）＜f（$\frac{x-b}{2}$），其中常数b∈R，试求实数x的取值范围．
18．若f（$\sqrt{x}+2$）=x+6$\sqrt{x}$+3，则f（x）=x2+2x-5，（x≥2）．
5．已知a=3，求$\frac{1}{1+{a}^{\frac{1}{4}}}$+$\frac{1}{1-{a}^{\frac{1}{4}}}$+$\frac{2}{1+{a}^{\frac{1}{2}}}$+$\frac{4}{1+a}$的值．
13．（x2+1）（$\frac{1}{{x}^{2}}$-mx）5展开式中x2项的系数125，求m的值．
14．一个等差数列的前n项和为48，前2n项和为60，则它的前3n项和为（　　）
A．-24B．84C．72D．36

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网