题目内容
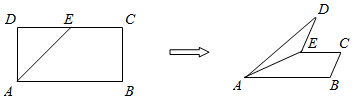
2．点G为△ABC的重心，设$\overrightarrow{BG}$=$\overrightarrow{a}$，$\overrightarrow{GC}$=$\overrightarrow{b}$，则$\overrightarrow{AB}$=（ ）| A． | $\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$ | B． | $\frac{3}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$ | C． | $\overrightarrow{b}$-2$\overrightarrow{a}$ | D． | 2$\overrightarrow{a}+\overrightarrow{b}$ |
分析 由题意作图辅助，从而利用线性运算求解即可．
解答 
解：由题意知，
$\overrightarrow{EB}$+$\overrightarrow{BG}$=$\overrightarrow{EG}$，
即$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{BG}$=$\frac{1}{2}$$\overrightarrow{GC}$，
故$\overrightarrow{AB}$=$\overrightarrow{GC}$-2$\overrightarrow{BG}$=$\overrightarrow{b}$-2$\overrightarrow{a}$，
故选C．
点评 本题考查了学生的作图能力及数形结合的思想应用．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
15．如果cotα=2，则sin2α的值是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
13．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，若F2关于渐近线的对称点为M，且|MF1|=$\sqrt{2}$c，则该双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | 2 |
7．
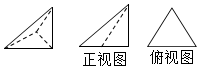已知三棱锥的直观图及正视图与俯视图如图，其中正视图是直角边为3的等腰直角三角形，俯视图是边长为3的正三角形，则该三棱锥侧视图的面积为（ ）
已知三棱锥的直观图及正视图与俯视图如图，其中正视图是直角边为3的等腰直角三角形，俯视图是边长为3的正三角形，则该三棱锥侧视图的面积为（ ）| A． | $\frac{9}{2}$ | B． | $\frac{9}{4}$ | C． | $\frac{9\sqrt{3}}{2}$ | D． | $\frac{9\sqrt{3}}{4}$ |
14．已知AB是单位圆上的动点，且|AB|=$\sqrt{3}$、单位圆的圆心为O，则$\overrightarrow{OA}•\overrightarrow{OB}$=（ ）
| A． | -$\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
11．已知m，n表示不同的直线，α，β表示不同的平面，则下列命题正确的个数是（ ）
①若m⊥α，n⊥α，则m∥n；
②若m⊥n，n⊥α，则m∥α；
③若m⊥β，α⊥β，则m∥α；
④若m⊥α，m⊥β，则α∥β．
①若m⊥α，n⊥α，则m∥n；
②若m⊥n，n⊥α，则m∥α；
③若m⊥β，α⊥β，则m∥α；
④若m⊥α，m⊥β，则α∥β．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
12．设集合P={x|x2+2x-8≤0}，$Q=\{y|y={（\frac{1}{3}）^x}，x∈（-2，1）\}$，则P∩Q=（ ）
| A． | $（-4，\frac{1}{9}）$ | B． | $（\frac{1}{9}，2]$ | C． | $（\frac{1}{3}，2]$ | D． | $（\frac{1}{3}，2）$ |